동쪽 오오단 나라에서는 초등학교 때 곱셈을 5x5까지만 외워도 된대요.
왜 동쪽인가... 서쪽에는 19단을 외우는 곳이 있으니 그 반대편 어딘가가 아닌가 했다는...
사실 그 반대편 어딘가는 미국 캘리포니아 정도 되겠네요. 속 편하게 5x5까지 외우면 되는 친구들이 찾아왔습니다. 외울 게 적어서 좋겠다는 생각이 들죠. 외울 게 이것밖에 안 됩니다.
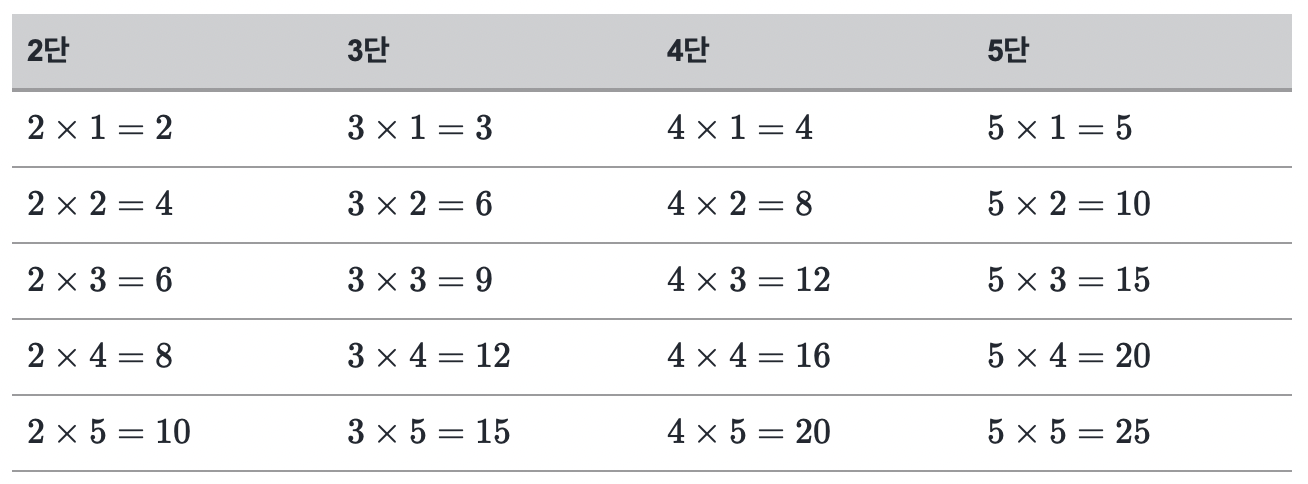
이 친구들에게 우리는 이미 다 아는
아뇨. 그렇게 할 수도 있었겠지만, 그 친구들은 딱 1번 더했다는군요.
어떻게?

7개씩 5줄을 놓은 다음에 다 세면 되겠죠. 하지만 다 세기가 귀찮아서 우리처럼 구구단을 아는 사람은 7개씩 5줄 있으면 35라는 것을 기억해 놓았다가 씁니다.
오오단만 외운 친구들은 이 문제를 이렇게 바라봅니다.
7개씩 묶어 놓은 것은 오오단에서 해 본 적이 없으니 7개씩 묶지 말고
5개씩 묶은 거 따로 세고 2개씩 묶은 거 따로 세어서
더하자
그러니까, 그림을 이렇게 보기로 한 거지요.
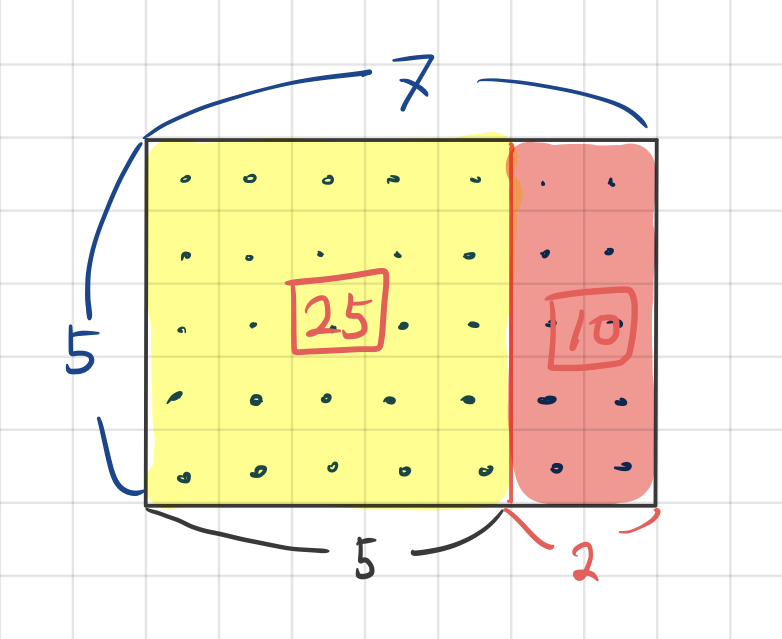
한꺼번에 세지 말고, 노란 부분을 세고, 빨간 부분을 센 다음, 둘을 합쳐도 한꺼번에 센 거랑 같을 거잖아요.
그런데 노란 부분은
그래서 25와 10을 합해서 (더하기 한 번) 35가 답이란 걸 찾아냈습니다.
방금 분배법칙(distributive property)이란 걸 해 본 겁니다. 이름은 난해하지만 주어진 곱셈에 따라 열 맞춰서 셀 것들을 늘어놓고, 한꺼번에 세지 말고 나누어서 센 다음 더해도 똑같은 답을 낼 수 있다는 것이죠.
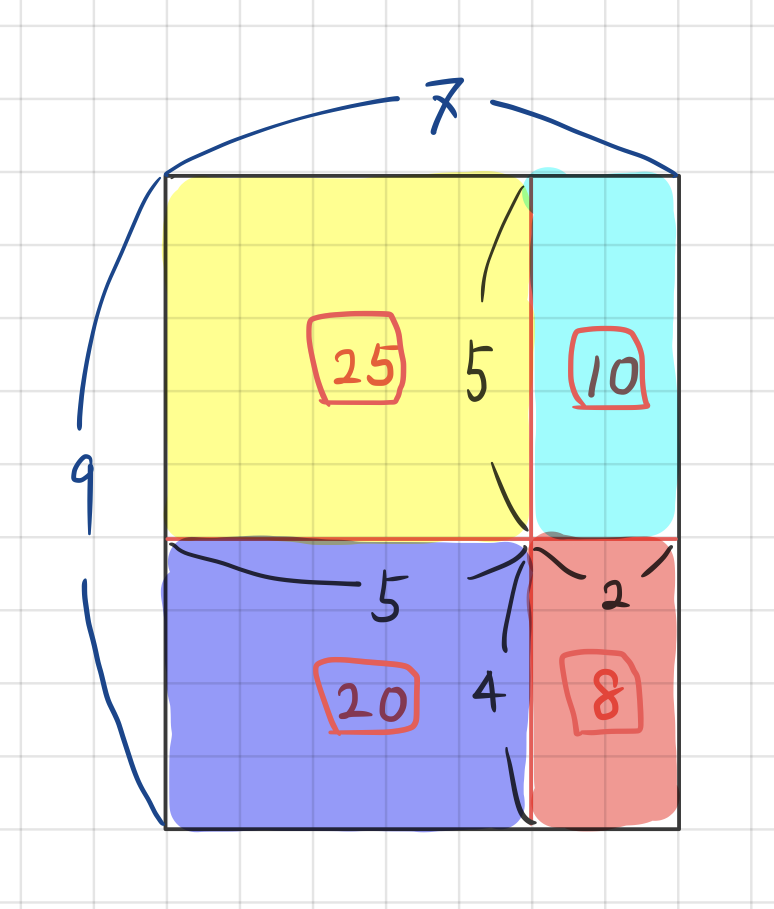
다 더하면
우리가 구구단에서 외운 거(
오오단 친구들이 곱셈 문제를 쪼개서 오오단에 나오지 않는 곱셈을 풀었듯이 우리도 곱셈 문제를 쪼개서 구구단에 나오지 않는 곱셈을 할 수 있게 됩니다.
생각해 보면 우리가 구구단만 알고 있지는 않아요. 구구단이라고 하는 것이 2단부터, 9단까지 있는 것인데, 사실 1단도 외울 필요가 없어서 따로 안 외우는 것 뿐이지 구구단 1단의 결과가 어떻게 되는 지는 다 알죠. 1에다가 무언가를 곱하면 그 무언가가 똑같이 나오니까요.
그리고 10단, 20단, 100단, 200단, 300단, 심지어 1000단도 이미 알고 있습니다. 이건 직관으로 알고 있는 것이죠. 예를 들어 200단이라고 하면 200개 각각을 생각하는 게 아니라 100이라 불리는 어떤 덩어리가 2개 있다고 생각해서 2단을 기준으로 다 계산하고 결과값은 100개를 한 묶음으로 생각한 것이었으니 결과값의 뒤에 0을 두 개 더 붙입니다. 사실 무엇을 한 덩어리로 생각하느냐에 따른 이야기일 뿐이지요.

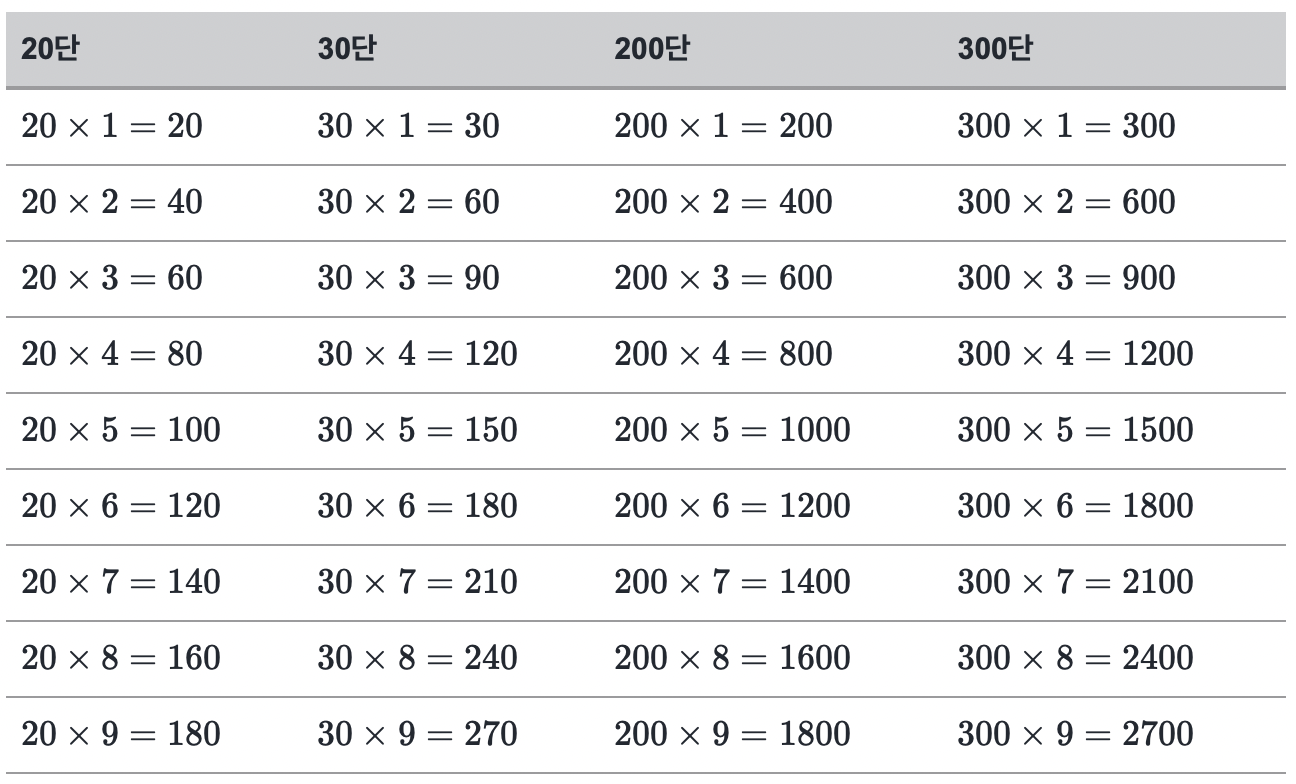
자 이제 우리가 모르는 곱셈 문제를 쪼개서 우리가 아는 걸로 풀어봅시다.
구구단까지 우리가 알고 있으니 9랑 6으로 나눌까요?
아니죠. 앞에서도 이야기했지만 10단도 알고 있습니다. 외우지 않았을 뿐이죠. 그래서 10과 5로 나눕니다. (사실 다른 방법으로 쪼개도 되지만 되지만 이것이 계산이 편합니다)
10과 5로 나누어서 생각하면

쪼갤 때마다 그림을 그릴 수는 없는 노릇이고, 몇 번 하다보면 머릿속으로도 어떻게 쪼개는 것이 잘 하는 것인지 금방 알게 됩니다. 앞에서 예로 든 15는 (10, 5) 뿐만 아니라 (9, 6)으로도 (8, 7)로도 쪼갤 수 있고, 그렇게 풀어도 같은 답이 나오지만, (10, 5)로 쪼개는 게 가장 편합니다. 복잡하게 계산할 필요 없이 15라는 숫자가 10과 5가 합쳐진 것이란 것은 쉽게 알 수 있으니까요.
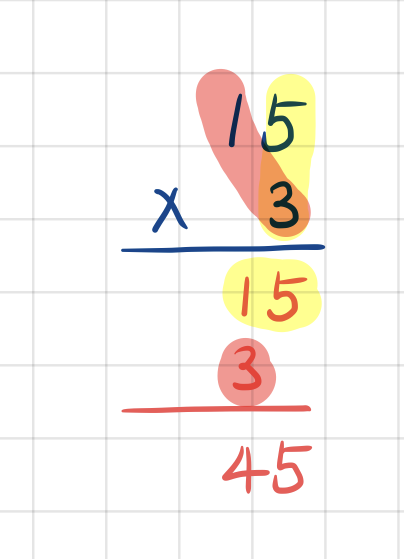
이제 이렇게 부분 계산한 것을 잘 배치해 봅시다. 곱셈을 세로로 쓴 후에, 첫번째 줄에는 5x3의 결과를 두 번째 줄에는 10x3의 결과를 써 줍니다. 그리고 마지막 줄에는 이 두 개를 합한 답을 적는 것이죠.

방금 우리는 곱셈의 세로셈을 완성했습니다.
앞으로도 반복해서 이야기할 것이지만, 수학자들은 잉크 아끼기에 열심입니다. 무언가 반복되거나, 바뀌지 않는 것이 생기면, 간략한 표현을 찾든지, 추상화하든지, 생략해버리죠.
앞의 세로셈을 잘 보면, 두 번째 줄의 결과값은 항상 맨 오른쪽 값이 0입니다. 그도 그럴 것이 몇 십(10, 20, 30, ...)에다가 무언가를 곱한 것이니 답도 몇 십이 나올 수 밖에 없겠죠. 끝자리가 항상 0이 나오므로 굳이 쓸 필요 없이 생략해 버립니다.

이렇게 생략을 하고 보니 두 번째 줄이 10 x 3 이 아니라 1 x 3인데 자릿수만 1이 위치하고 있던 십의 자리에 맞춰서 써 준 것 같이 보입니다. 그리고 10x3보다 1x3이 머리로 생각하기가 더 편하죠. 그래서 이제부터는 그냥 1x3을 하되 자릿수만 칼 같이 맞춰주기로 전략을 바꿉니다.
생각보다 많은 사람들이 이 부분을 모릅니다. 실제로 몇 십(10, 20, 30, ...)을 곱하는 것이었고, 그래서 오른쪽에 0이 다 달려 있는 숫자를 생략한 것 뿐이란 것을요. 그래서 초등학생들이 자주하는 실수가 0이 생략된 걸 모른 채 그냥 더해서 틀리는 겁니다. 이제 왜 세로셈 곱셈 전략을 이렇게 가져왔는지 알았으니 우리는 이러지 맙시다.

여기서 잉크를 한 번 더 아낄 수 있습니다. 굳이 쪼갠 결과를 다 써 놓고 더해야 할까? 라는 것이죠. 쪼갠 결과를 더하는 과정을 보면, 둘째 줄의 일의 자리가 항상 0 (그래서 우리는 쓰는 걸 생략하기까지 했죠)이므로 최종 답의 일의 자리는 첫째 줄의 일의 자리와 같습니다. 무언가를 합해야 하는 건 십(10)의 자리에서 일어나는 일이지요.
그래서 첫번째 결과의 일의 자리는 최종답에 바로 적고, 그것의 십의 자리는 기억을 해 두기 위해서 어딘가에 작게 표시해 둡니다. 둘째줄 계산을 할 때 나온 값이랑 아까 표시해 둔 답을 더해서 최종 답에 씁니다.
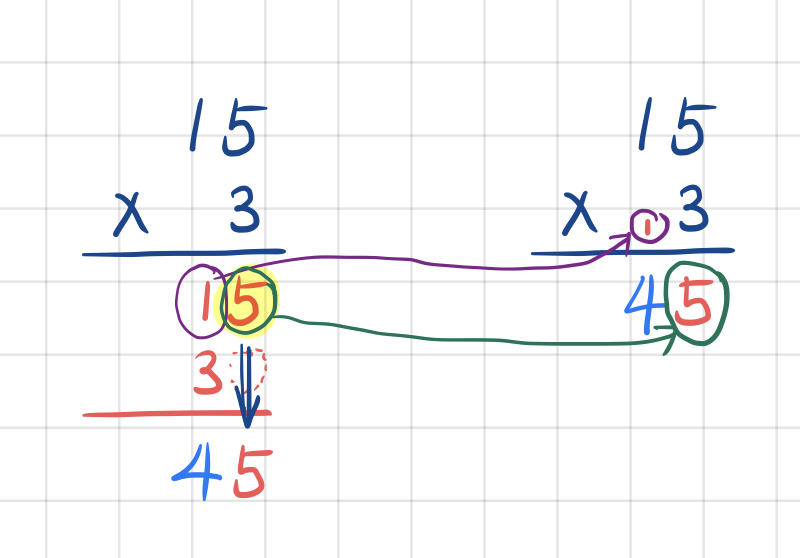
이렇게 해서 곱셈 계산을 한 줄에 할 수 있게 된 겁니다. 이 방식대로 조금만 확장하면, 여러자릿수 곱하기 한자릿수 곱셈을 한 줄에 할 수 있게 됩니다. 123 x 3은 어떻게 쪼개냐구요?

이제 배치해보고, 잉크를 아껴보세요.
구구단 배우고 바로 다음에 배우는 10이상되는 숫자들의 곱셈을 할 때에 사실 우리는 이미 분배법칙을 사용하고 있었습니다. 아마 스쳐지나가듯 넘어갔거나 곱셈하는 방법만 익히고 넘어갔을지도 모르겠지만요.
나눗셈도 분배법칙 이용해서 답을 내도록 초등학교 때 훈련 받았습니다. 분배법칙이란 이름만 숨긴 채로요. 기회되면 그것도 살펴보도록 하죠. 끝.
