응? 갑자기 왜 물리를?
일차함수(linear function)랑 비율(ratio) 좀 배우고 나서 왜 이리로 건너왔느냐..
그 정도만 이해해도 할 만해서 그런 것이고
결론부터 이야기하자면 오늘은 아래 두 식을 이해하게 될 것이다.
하지만 외울 필요는 없고, 이해만 하면 된다. 다만 속도 - 시간 그래프(v-t Graph)에서, 주어진 속도/가속도/시간에 따라 그래프가 어떻게 그려지는지 아는 것은 필수.
그럼 등가속도 운동이란?
단어를 하나하나 뜯어보면 모르는 말은
등 이랑 가속도 정도 되겠다.(운동은 알잖아?)
등 (같을 등 等, uniformly)
가속도 (accelerated)
운동 (motion)
자, 그럼 가속도란?
가속도: 속도 의 시간당 변화율
자. 어디서 많이 본 모양새이다. 이전에 배웠던 속도는 뭐라 그랬더라?
속도: 거리 의 시간당 변화율
그리고 간단히 수식으로는 이랬었다.
패턴이 똑같으니 가속도도 비슷한 방법으로 쓸 수 있겠지. 이렇게
식에서 알 수 있듯이 1초 동안에 속도가 얼마나 바뀌었는지 비율로 나타낸 값이 가속도이다.
예를 들어 처음에는 속도가 10m/s 이었는데, 2초 후에 50 m/s가 되었다면 속도 변화량
여기서 주의할 것은 지난번 속도를 계산할 때 그랬던 것처럼 가속도를 계산할 때에도 속도의 변화량을 그것이 변하는 데 걸린 시간(시간 변화량)으로 나누어야 한다는 것이다. 걸린 시간은 직접적으로 주어질 때도 있고, 이렇게
2초 걸렸다
아니면 걸린 시간을 유추할 수 있게 주어지기도 한다. 이렇게
처음 속도를 잴 때 시계는 3초를 가리켰는데, 나중 속도를 잴 때 보니 5초를 가리키더라
?! 원래 식은
속도 시간 그래프를 그리기 전에, 우리가 익숙한 x, y로 표현된 1차식을 한 번 보자.
(0, 1)과 (2, 5)를 지나는 1차함수를 찾고 그래프로 그리시오
기분좋게도, x=0일 때의 y값이 1로 주어져 있으니 y 절편 (y-intercept)는 힘들이지 않고 찾았다. 그럼 1차 함수는
1차 함수에서 기울기는 어떻게 구하던가?
그러므로 직선 식은

복습은 여기까지 하고, 속도와 시간으로 다시 돌아오자.
처음(t=0 )에 속도를 재었더니 1 m/s 였는데, 2초 후에(t=2 )에 속도를 재었더니 5 m/s 로 속도가 바뀌었더라
관계식을 찾고 가로축을t , 세로축을v 로 하는 그래프로 그리시오
여기서 눈치챌 수 있으면 빠른 것임 :-) 처음에 나왔던 문제랑 완전히 같은 문제이다.
(0, 1)과 (2, 5)를 지나는 1차함수를 찾고 그래프로 그리시오
가로축이 시간

익숙한 그래프가 나오는 것 말고도, 속도-시간 그래프는 재미있는 성질이 있다. 바로 이것.
정말 그런가? 직선의 기울기는
아까 가속도 계산했을 때 값이 2m/
이 부분은 바로 이해하기 쉽지 않으니 직관을 동원해서 설명해야겠다.
쉬운 예제로 등속(속도가 같은) 운동에서 속도와 시간이 주어졌을 때 거리를 구하는 문제를 생각해 보자.
예를 들어 5m/s의 속도로 2초동안 움직이면
그럼 이것을 속도-시간 그래프로 그리면 어떻게 될까? 등속 5m/s 라는 것은 시간이 0초이든 1초이든 2초이든 항상 속도가 5m/s 이라는 이야기니까, 속도-시간 그래프로 그리면

이 그래프에서 0초에서 2초 사이에 만들어지는 직사각형 넓이가
아마 이게 우연이 아니라는 건 눈치를 챘을 것이고, 등속이 아니고 다른 경우에도 되는 지 확인해 볼까?
0초에서 1초가 될때까지는 2m/s의 속도로 가다가 1초에서 2초 사이에는 4m/s의 속도로 이동했다면 총 이동 거리는 어떻게 될까?
0에서1초 사이에는
1에서2초 사이에는
따라서 6m가 된다.
그래프로 그려보면
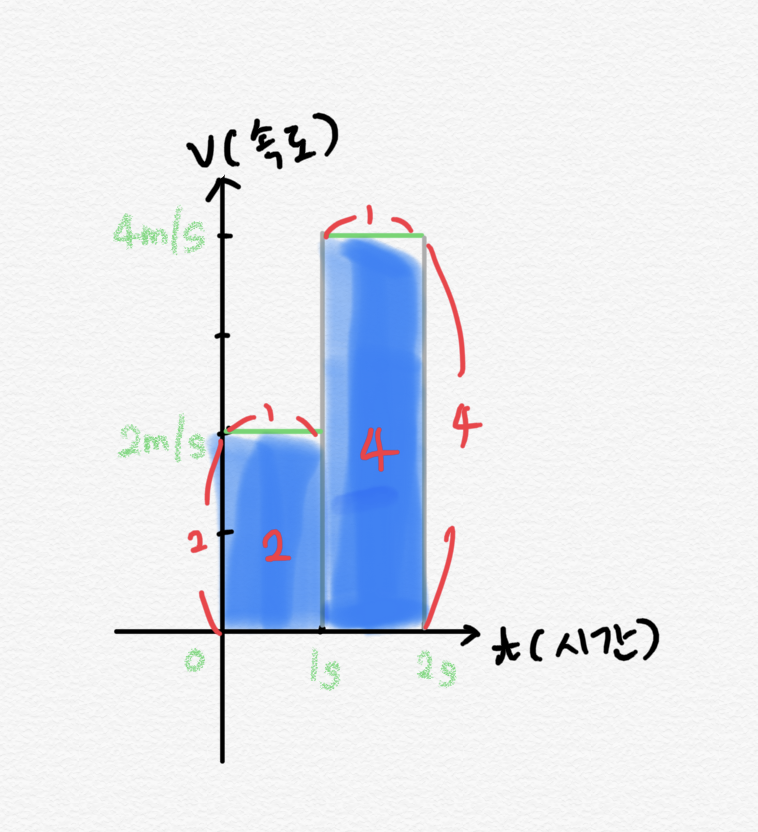
이번에도 아래쪽 면적이 다 합해서 6이 되어서 이동 거리가 된다.
같은 방법으로 시간에 따라 속도가 계속 바뀌더라도 그 바뀌는 포인트마다 구간을 나누어서 속도와 그 속도가 유지되던 시간을 곱하면 그 시간 동안 이동한 거리를 구할 수 있고, 그것을 다 더하면 총 이동 거리가 나온다.
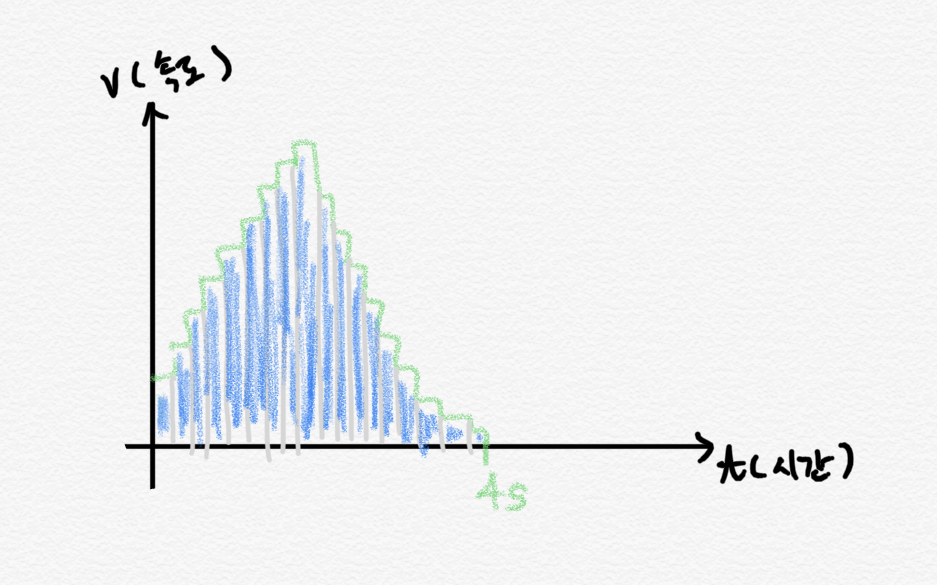
마찬가지로 그래프에서는 각 구간에 만들어진 직사각형의 넓이가 그 구간에서의 이동 거리가 되고, 각 직사각형의 넓이를 모두 합하면 총 이동 거리가 나온다. 여기서 모든 직사각형의 넓이의 합은 그래프 아래쪽 면적과 같다. 그래서 그래프 아래쪽 면적이 이동 거리가 된다.
이제 이 사실을 이용해서 등가속도 직선운동에서의 이동 거리를 구하는 공식을 유도해보자.
처음에 속도가
그래프로 그려보면 이렇게 된다.
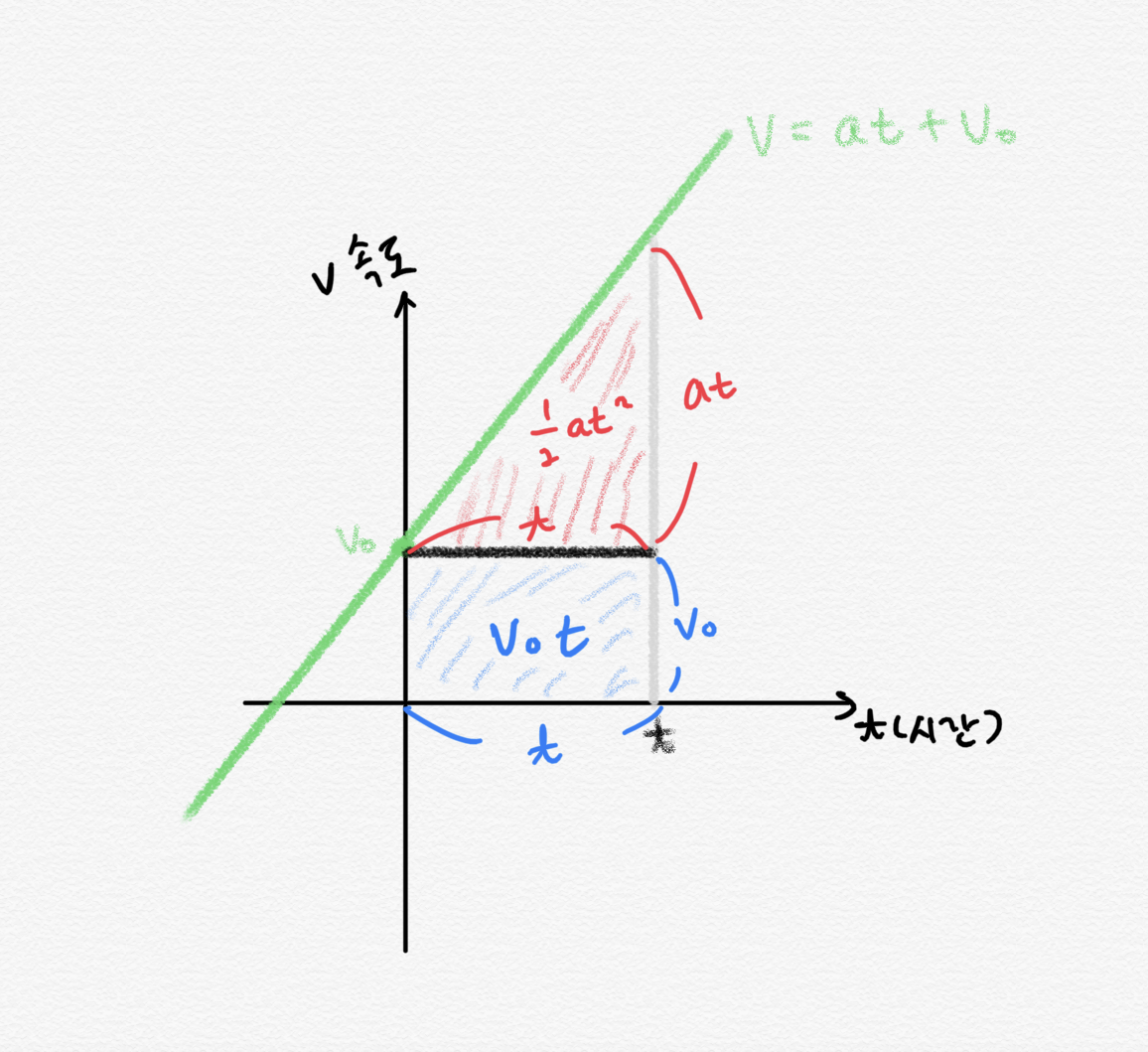
시간 0초에서
굳이 나누지 않고 사다리꼴 넓이 구하는 방법으로 바로 구해도 된다. 사다리꼴의 넓이는

처음에 가만히 놓았다고 했으니 처음에는 속도가 0이다(
그럼 그 때 물체의 속도는 어떻게 되나?
30m/s라는 게 감이 잘 안 올 것이다. 10m/s가 사람이 달릴 수 있는 거의 최고 속도이다. 이걸 km/h로 환산하면 얼마게?
사람이 달리는 최고 속도는 시속 36 km/h 정도 된다. 30 m/s는 이것의 3배니까 시속 100km/h가 넘는 것이지. 그래서 고층에서 물건 던지면 안 되는 것이다.
오늘은 여기까지.
