인간이 다른 동물과 구분되는 특징 중의 하나는 세상을 숫자로 추상화 할 수 있는 능력이다. 들판에 있는 양 5마리와 뒷산에 나무 5그루 사이의 공통점을 파악하는 능력. 우리는 너무 당연하게 "5개네?" 하고 받아들이지만 다른 동물들에게는 힘든 그 과정 말이다.

우리는 방금 양 5마리와 나무 5그루라는 전혀 다른 상황을 숫자 5로 추상화했다.
양이 두 마리 도망갔다. 남은 양은 몇 마리? 3 마리다. 나무가 번개 맞아서 2개다 타서 쓰러져버렸다. 멀쩡한 나무는? 3 그루다. 그런데 이걸 우리가 어떻게 알고 있는지 신기하지 않은가? 양이 도망갈 때마다 남은 양이 몇 마리인 지 세어보지 않았고, 멀쩡한 나무도 다시 세어본 적이 없는데, 우리는 이걸 어떻게 아는가?
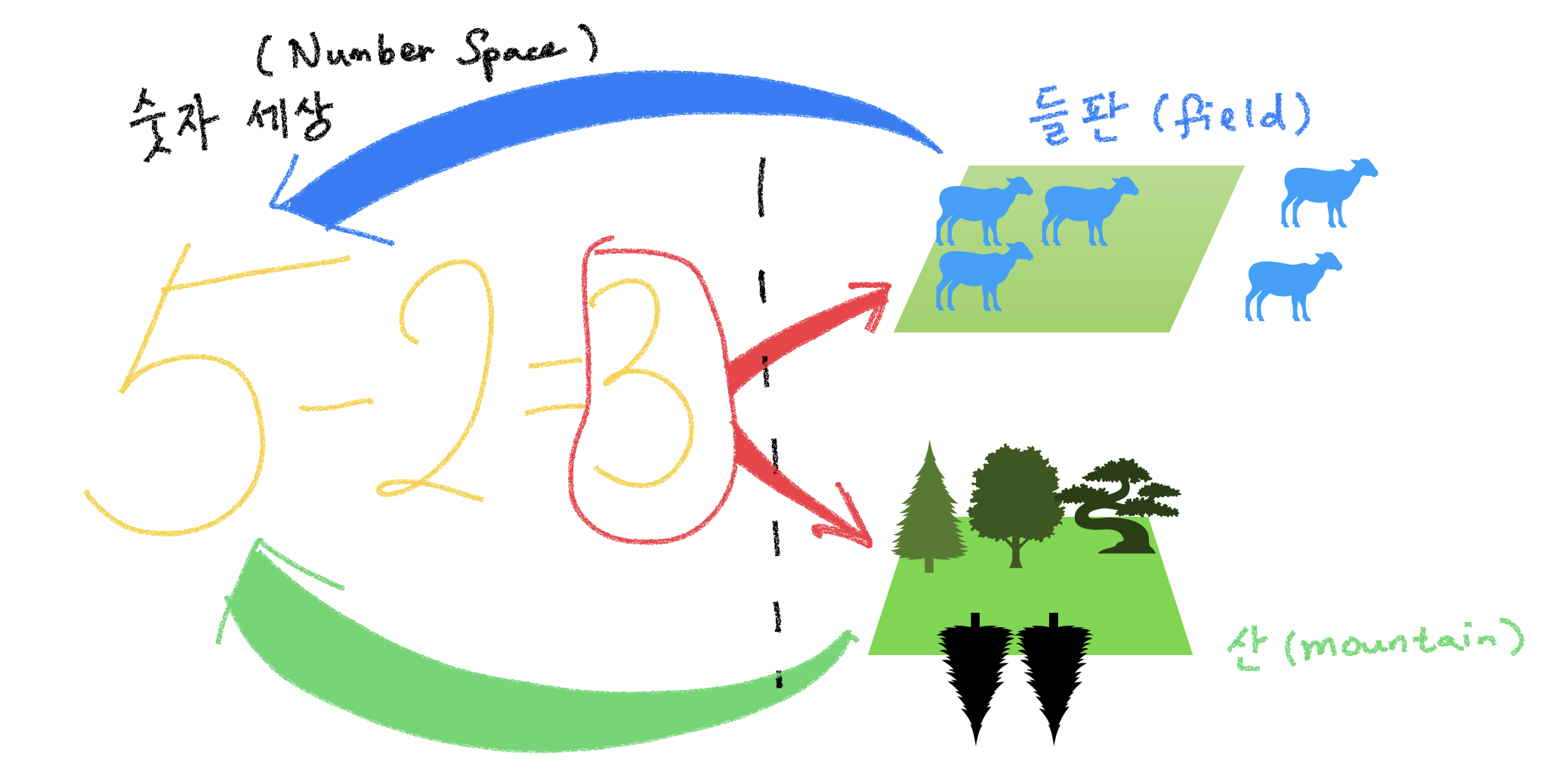
우리는 들판과 동산이라는 서로 다른 공간에 있던 양과 나무를 세어서 숫자 공간으로 가져온 다음에 숫자 공간에서 계산을 끝내고 그 결과를 들판과 동산으로 가져간 것이다.
우리에게 이런 추상화 능력이 없었다면, 각각의 상황에 대해서 하나씩 세고 앉아 있었을 것이다. 이것들이 사실은 한가지 원리라는 것을 알아내는 것은 대단한 통찰이다.
숫자 공간에서 계산하기는 어렸을 때 지겹도록 반복해서 풀던 계산문제로 훈련했었고, 말로 설명되어 있는 상황을 수의 공간으로 가져오고 그 결과를 다시 말로 설명하는 것은 이른바 서술형 문제(word problems)를 풀면서 훈련했던 것이다.
대수학도 이런 과정의 연장선상에 있다. 중등 교과 과정에서 중점적으로 보는 대수학은 정의역이 하나의 변수로 되어 있는 선형대수(Linear Algebra)이고
그럼
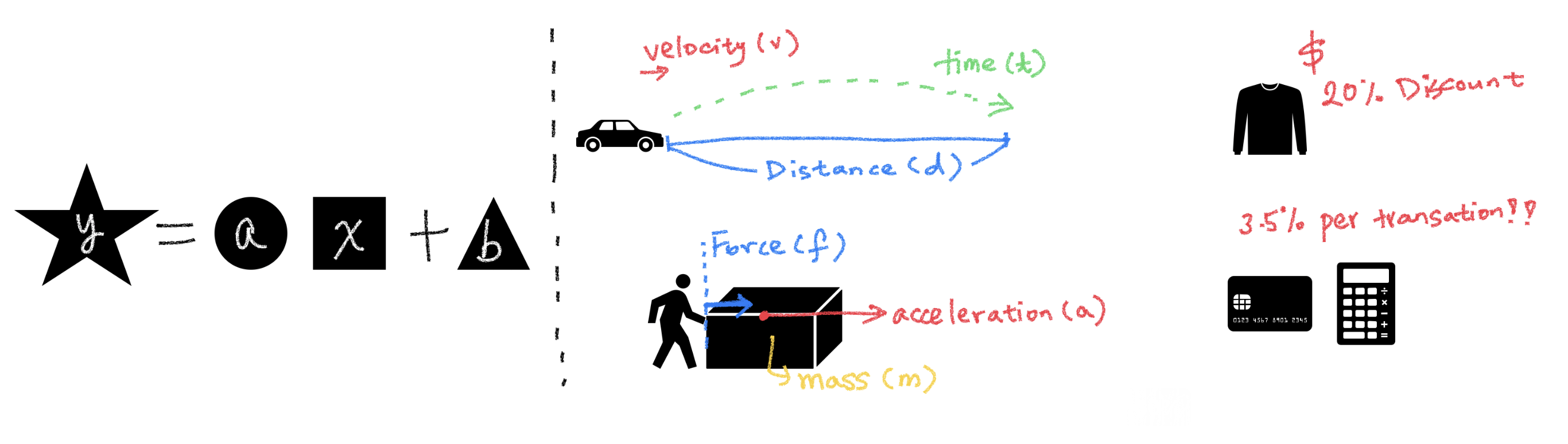
속력(
양변에
뉴턴 제 2 법칙이
옷 가게에서 팔고 있는 모든 옷을 20% 세일한단다. 옷의 원가를
가게를 하나 열었다. 현금 거래만 할 수는 없으니, 신용카드 결제를 받아야 할 텐데, 결제 회사 A에서는 건당 30센트의 고정 수수료에다가 결제금액의 3.5%를 수수료로 청구한다. 결제 회사 B는 한 달에 280달러의 회원비를 받지만 건당 고정 수수료는 없고, 결제금액의 2.8%를 수수료로 청구한다. 나는 대략 10달러짜리 악세서리를 팔 생각이다. 얼마 팔 지 못할 때에는 직관적으로 A결제회사를 이용하는 게 수수료를 적게 내는 방법이다. B 결제 회사를 이용하는 게 이득이 되려면 나는 한달에 몇 개 이상을 팔아야 하는 걸까?
A 회사를 이용할 경우 수수료를 y라고 하고 한달 판매 갯수를 x라고 하면
B 회사의 경우
B가 더 이득이려면
즉 757개를 팔 수 있을 때부터 B 결제 회사를 이용하는 게 이득이다. 꼭 부등식을 풀지 않더라도 각 선형관계식을 그래프로 그리면 어느 대략 어느지점부터 B회사 수수료가 더 작아지는 지 눈으로도 확인할 수 있다.

이와같이 선형대수만 가지고도 여러가지 현상을 하나의 모양으로 축약시킬 수 있다. 우리가 이것을 할 수 없었다면, 모든 상황 각각을 하나씩 세어보거나 하나하나 다양한 숫자를 넣어 보면서 매우 비효율적으로 상황판단을 하고 있었을 것이다. 능숙하게 다룰 수 있는 도구(선형대수)를 가진 사람은, 이 상황에 그 도구를 쓸 수 있는지만 알면 정말 작은 노력으로 그 상황을 이해하거나 다룰 수 있게 된다.
선형대수만 하면 심심하니, 2차식으로 나타난 것들은 어떤게 가능한 지 한 번 살펴보자.
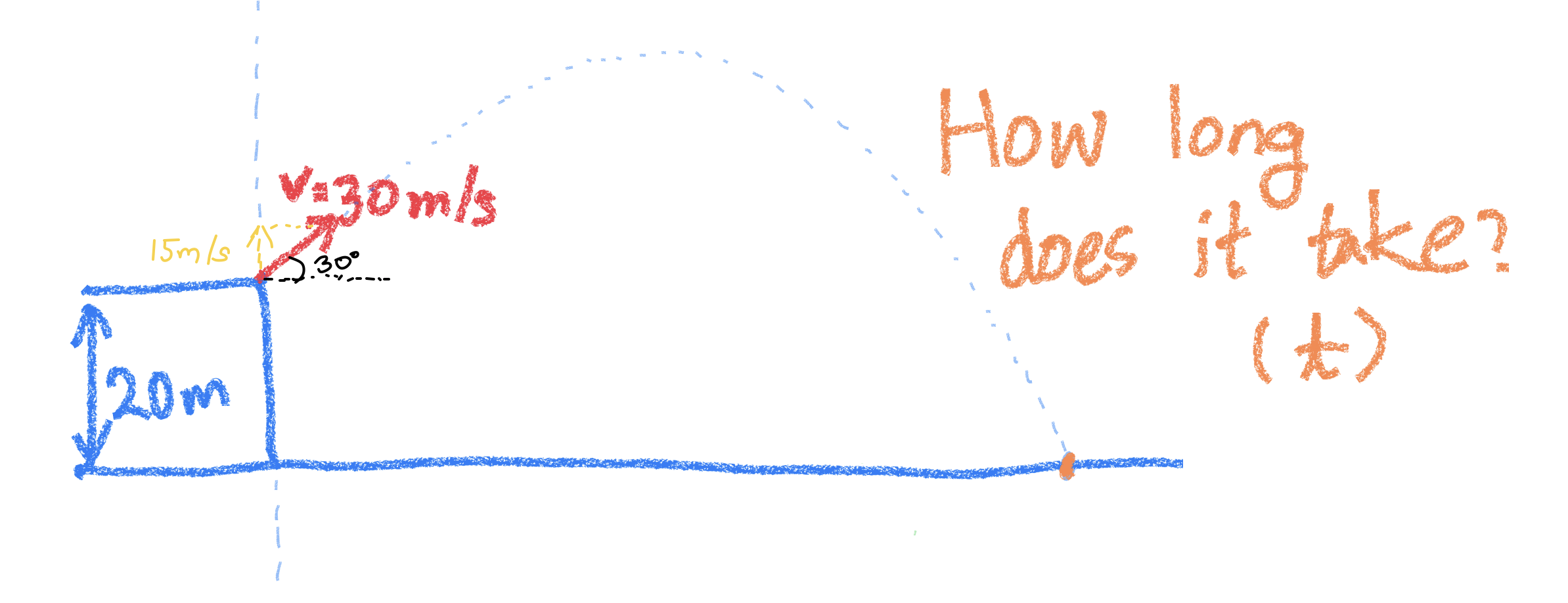
바닥에서 20m 높이에 있는 건물에서 공 하나를
바닥으로부터 공까지의 거리를
공이 바닥에 떨어지면 바닥과 공 사이의 거리
여기서 재미있는 것은 이렇게 숫자의 공간에서 나온 답을 다시 원래 세상으로 가져올 때의 일이다. 답이 두 개인데, 4초 후에 땅에 떨어진다는 이야기까지는 이해가 가지만, -1초 후라는 것은 도대체 무슨 말인가? 문제 설정이랑 안 맞으니까 무시하면 되는 걸까?

-1 초 후라는 것은 1초 전이라고 해석할 수 있다. 1초 전에는 무슨 일이 일어났다는 걸까. 문제에서는 20m 높이 건물에서 던진 것이지만, 만약에 이 물체가 그 전에 던져진 것이고, 우연히 지금 20m 건물을 윗방향
중고등 수학에 나오는 대수학은 세상을 해석하는 좋은 도구들을 하나씩 배워간다는 기분으로 접근하면 좋겠다. 좋은 도구가 이것만 있는 건 아니지만 말이다.
