7, 11, 13 배수 판별법 및 그 증명(Divisibility Rules and Proof for 7, 11, 13)

이전 글에서 7, 11, 13으로 나누었을 때 나머지를 구하는 법을 알아 보았다. 11은 자리마다 더하고 빼기를 반복하니 쓰기 쉬웠지만, 7, 13은 세자리씩 끊어서 더하고 빼기를 해야 하니 계산이 복잡한 것이 사실이다. 그런데 나머지를 구하는 것이 목적이 아니라, 나머지가 0이 되는 경우, 즉, 나누어 떨어지는 지 알아보는 것에는 좀 더 쉬운 방법이 있다.

나머지 구하는 법을 배우고 나서도 7, 13으로 나눈 나머지를 구하는 과정은 좀 까다로웠을 것이다. 그래도 기억해 놓도록 하자. 이 글에서 나누어 떨어지는 경우에 쓸 수 있는 더 쉬운 방법을 알아볼 테지만, 앞서 배운 3자리씩 끊어서 더하고 빼는 방식을 섞어서 쓰면 큰 숫자에 대해서 더 효율적으로 확인할 수 있게 되니 알아두면 요긴하다. 

각설하고, 주어진 숫자가 7, 11, 13으로 나누어 떨어지는 지만 확인하려면 이렇게 하면 된다. 방법이 셋 다 비슷하다는 것에 놀란다.

이 숫자 셋은 왜 이렇게 붙어다니는지...

7로 나누어 떨어지는 지 확인하는 법

맨 마지막 자리를 제외한 숫자에다가 맨 마지막 자리를 2배한 숫자를 뺀다. 그 숫자가 7의 배수, 즉 7로 나누어 떨어지면, 원래 숫자도 7의 배수이다. 이것은 계속 반복해도 되기 때문에 한 눈에 7의 배수가 보일 때까지 계속 반복하면 된다.

11로 나누어 떨어지는 지 확인하는 법

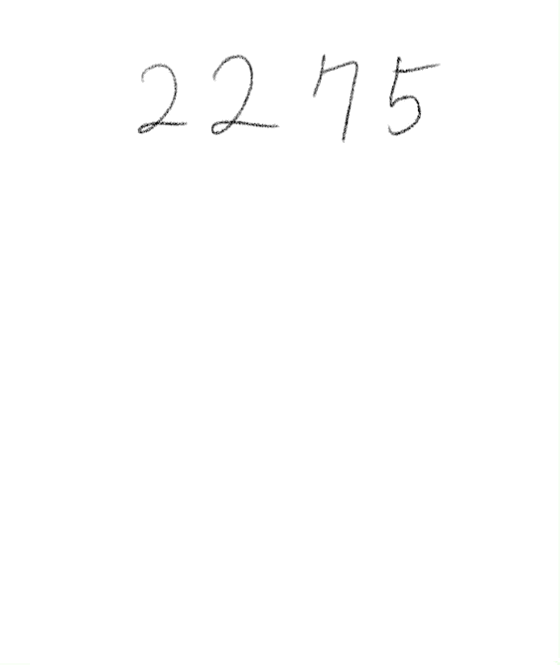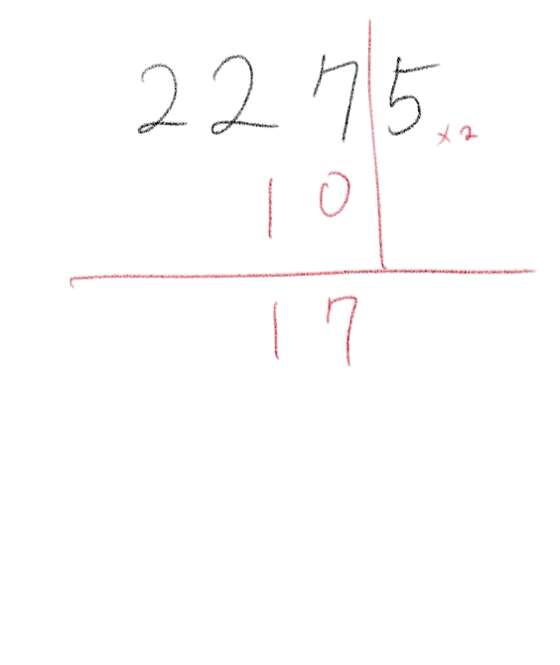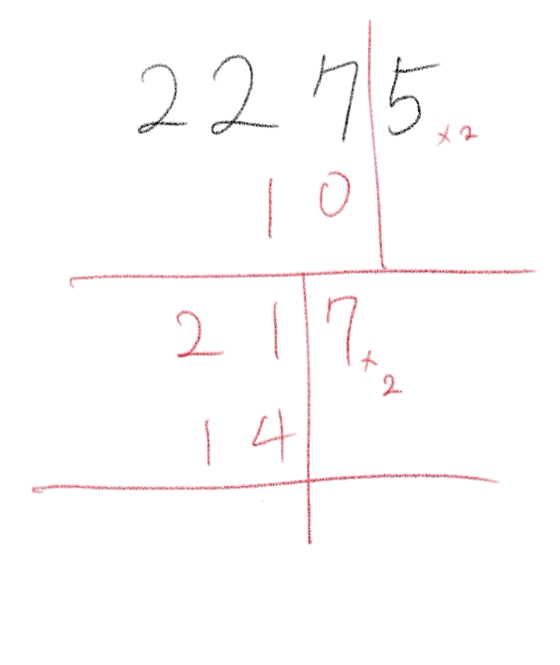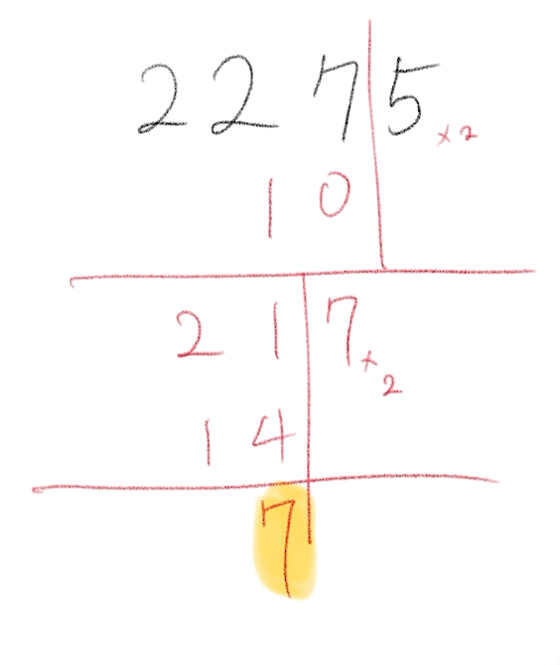
맨 마지막 자리를 제외한 숫자에다가 맨 마지막 자리의 그 숫자를 뺀다. 그 숫자가 11의 배수이면 원래 숫자도 11의 배수이다. 이것은 계속 반복해도 되기 때문에, 한 눈에 11의 배수가 보일 때까지 계속 반복하면 된다.

13으로 나누어 떨어지는 지 확인하는 법

맨 마지막 자리를 제외한 숫자에다가 맨 마지막 자리의 숫자를 4배한 숫자를 더한다. 그 숫자가 13의 배수이면 원래 숫자도 13의 배수이다. 이것은 계속 반복해도 되기 때문에, 한 눈에 13의 배수가 보일 때까지 계속 반복하면 된다.

왜 이렇게 되나?

바로 설명 시작하기 전에 힌트로 시작해 보자. 이것만 가지고 저렇게 되는 법을 알 수 있을까?

 20 = 3 \times 7 -1 

 10 = 11 - 1 

 40 = 3\times 13 + 1 

뭔가 알 것 같으면 스크롤을 멈추고, 공책을 꺼내서 써 보자 :)

7의 배수 판별법 증명

문자로(대수적으로) 증명하기 전에 숫자 예제로 먼저 해 보자. 첫 번째 예제 2275는 2\times 1000 + 2\times 100 + 7 \times 10 + 5 로 나타낼 수 있다. 이 숫자가 정말로 7의 배수라면 7 \times \text{something} 형태로 나올 것이다. something이라고 길게 쓰면 잉크가 아깝기 때문에 k라고 줄여 쓰면,

 \begin{aligned}2\times1000+2\times100+7\times10+5&=7k\\ 2\times1000+2\times100+7\times10+5 - 5\times21&=7k-5\times21\\ 2\times1000+2\times100+7\times10 - 5\times20&=7k-5\times21\\ 10\times(\underbrace{2\times100+2\times10+7 -5\times2}_A)&=\underbrace{7k-5\times3\times7}_\text{7의 배수}\end{aligned}  

10에다가 무언가를 곱한 것이 7의 배수가 된다는 게 무슨 말일까? 그 무언가를 위에서 처럼 A라고 하자. 7과 10은 서로소(coprime, 공약수가 1외에는 없는 두 숫자)이기 때문에, 10 안에는 7의 배수가 될 만한 게 있을 수가 없으니, A가 7의 배수가 되어야만 10 곱하기 A가 7의 배수가 된다. 그러므로 2\times 100 + 2\times10 + 7 - 5\times2 가 7의 배수이다. 말로 풀면, 원래 숫자의 마지막 자리를 뺀 숫자( 227 )에서 마지막 자리 숫자의 두 배 ( 5\times2 ) 를 뺀 숫자가 7의 배수가 된다는 이야기이다.

이제 이것을 문자를 도입해서 일반화해 보겠다. 일의 자리 숫자를 a_0 십의 자리 숫자를 a_1 , 그런 식으로 해서 10^n 자리 숫자를 a_n 이라고 하자. 그러면 주어진 자연수는 다음과 같이 나타낼 수 있다.

 10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1+a_0 

 예를 들어 앞에서 든 예제인 2275라면, a_3=2, a_2=2, a_1=7, a_0=5 이므로 다음과 같이 쓸 수 있을 것이다.

 10^3\times2+10^2\times2+10^1\times7+5  

다시 원래 일반식으로 돌아가서, 아까 쓴 트릭에 가까운 전개과정을 한 번 적용해 보겠다. 원래 숫자가 7의 배수라면 그 숫자의 마지막 자리, 즉 1의 자리의 값 a_0 을 21번 빼준 것도 7의 배수이다. 왜냐하면 21이 7의 배수이므로 a_0\times21 도 7의 배수이고, 원래 숫자가 7의 배수라면 거기에 7의 배수인 a_0\times21 을 빼도 7의 배수이기 때문이다. 이것을 정리하면 다음과 같이 된다.

 10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1+a_0=\underbrace{7k}_\text{7의 배수} 

 10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1+a_0-21a_0=\underbrace{7k-21a_0}_\text{역시 7의 배수}  

그런데 신기한 일은 좌변(left side)에서 일어난다. 원래 자연수에서 일의자리를 뺀 나머지는 10의 배수이다. 일의자리가 0일 때에만 전체 숫자가 10의 배수가 되는데, 원래 1의 자리숫자 a_0 에서 21a_0 을 빼면, -20a_0 이 되므로 1의 자리가 사라진다. 십의 자리만 원래 값보다 2가 줄어들게 된다.

 \underbrace{10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1-20a_0}_\text{10의 배수}=\underbrace{7k-21a_0}_\text{역시 7의 배수}  

 10\times(\underbrace{10^{n-1}a_n+10^{n-2}a_{n-1}+\cdots+a_1-2a_0}_\text{1의 자리를 제외한 숫자에서 1의자리의 두배를 뺀 값})=\underbrace{7k-21a_0}_\text{역시 7의 배수}  

좌변을 10으로 묶으면 남는 모양이 원래 숫자에서 1의자리를 제외하고 만든 숫자에다가 1의자릿값의 두 배를 뺀 값이 된다. 10에다가 그 숫자를 곱해서 7의 배수가 된다는 것은 그 숫자가 7의 배수가 될 때만 가능하다. 그러므로 1의 자리를 제외한 숫자에서 1의 자릿값의 두 배를 뺀 값이 7의 배수이면, 원래 숫자도 7의 배수이다.

다 써 놓은 게 눈 앞에 있으면 어떻게 따라가기는 하겠는데, 애초에 저런 증명은 어떻게 만드는 건가요?

음.. 라마누잔이 아니고서야, 문제를 보자마자 짠 하고 나오기는 힘든 노릇이다. 일단 종이에다가 연필로 몇 가지 예제를 끄적거려 보는 게 처음으로 할 일이고, 두 번째로는 말로 설명된 것을 문자로 나타내는 게 중요하다. 사실 7의 배수 판별법의 증명은 7의 배수 판별법 자체를 대수로 나타내는 것으로부터 증명이 나아가야 하는 방향을 거의 다 잡을 수 있다.

"어떤 자연수가 7의 배수인 것을 판별하려면 그 자연수의 일의 자릿수를 제외한 숫자에서 일의 자릿수의 2배를 뺀 숫자가 7의 배수인지 판별하면 된다."

라는 문장을 하나하나 뜯어서 대수적으로 나타내어 보자.

"어떤 자연수가 7의 배수이다" \Longleftrightarrow 10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1+a_0=7k 

(1)번 등식이라고 하자.

"그 자연수에서 1의자리 빼고 나머지 부분으로 만든 숫자에 1의자리 2배를 뺀 숫자가 7의 배수이다" \Longleftrightarrow 10^{n-1}a_n+10^{n-2}a_{n-1}+\cdots+a_1-2a_0=7l 

(2)번 등식이라고 하자

우리가 증명하고 싶은 것은 (1)이랑 (2)가 같은 말이라는 것이다. 여기까지 써 놓고 출발하는 것이다. 그러면 증명 방향이 눈에 보인다. (2)식에다가 양변에 10배를 하면 (1)식이랑 상당히 비슷해지는 것을 알 수 있다.

 10^{n}a_n+10^{n-1}a_{n-1}+\cdots+10a_1-20a_0=70l 

 차이를 보면 (1)식은 a_0 로 끝나는데 (2) 식은 -20a_0 로 끝난다는 것이다. (1)식에서 21a_0 를 빼서 (2)가 만들어졌다는 것을 여기서 알 수 있다. 그리고 그것을 아는 순간, 21이 7의 배수니까, 21a_0 를 빼도 원래 숫자가 7의 배수라면 여전히 7의 배수가 된다는 걸 알 수 있게 된다. 

배수 판별법을 써 놓고 그걸 증명하는 건 고민해서 한다고 쳐요. 배수 판별법 자체는 어떻게 만든 거죠?

좋은 질문이다. 배수 판별법을 증명하는 것 보다 배수 판별법 자체를 만드는 데 더 비상한 아이디어가 필요하다. 이건 어떻게 만든 걸까? 

앞에 힌트로 주었던 것을 포함해서 중요한 단서를 나열해 보면

1. 원래 숫자에서 7의 배수를 더하거나 뺀 숫자를 7로 나눈 나머지는 원래 숫자를 7로 나눈 나머지와 같다.

2. 일의 자리 a_0 를 없애고 싶으면, a_0 를 빼든지, 11a_0 를 빼든지, 21a_0 를 빼든지 31a_0 를 빼든지, ..., 더해서 없애고 싶으면 9a_0 를 더하든지 19a_0 를 더하든지 29a_0 를 더하든지...

이제 단서 1과 2를 동시에 만족하는 것은? 21a_0 를 빼는 것이다. 7의 배수를 빼는 것이면서 동시에 1의 자리를 없애버릴 수 있으니 말이다.

11의 배수 판별법 증명

1. 원래 숫자에서 11의 배수를 빼거나 더해서 만든 숫자를 11로 나눈 나머지는 원래 숫자를 11로 나눈 나머지와 같다.

2. 마지막 자리 a_0 를 없애고 싶으면, a_0 를 빼든지, 11a_0 를 빼든지, 21a_0 를 빼든지, 31a_0 를 빼든지, ..., 더해서 없애고 싶으면 9a_0 를 더하든지 19a_0 를 더하든지 29a_0 를 더하든지... 

단서 1과 2를 동시에 만족하는 것은 11a_0 빼는 것이다.

 \begin{aligned}10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1+a_0&=\underbrace{11k}_\text{11의 배수}\\ 10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1+a_0-11a_0&=\underbrace{11k-11a_0}_\text{11의 배수}\\ 10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1-10a_0&=\underbrace{11k-11a_0}_\text{11의 배수}\\ 10\times\underbrace{(10^{n-1}a_n+10^{n-2}a_{n-1}+\cdots+a_1-a_0)}_\text{1의 자리를 제외한 숫자에서 1의 자리를 뺀 수}&=\underbrace{11k-11a_0}_\text{11의 배수}\end{aligned} 

 10과 11은 서로소이기 때문에 "1의 자리를 제외한 숫자에서 1의 자리를 뺀 수"가 11의 배수가 아니고서는 윗 식이 성립할 수가 없다. 그러므로 "1의 자리를 제외한 숫자에서 1의 자리를 뺀 수"가 11의 배수인지 확인해서 원래 숫자가 11의 배수인지 확인할 수 있다.

13의 배수 판별법 증명

1. 원래 숫자에서 13의 배수를 빼거나 더해서 만든 숫자를 13으로 나눈 나머지는 원래 숫자를 13으로 나눈 나머지와 같다.

2. 마지막 자리 a_0 를 없애고 싶으면, a_0 를 빼든지, 11a_0 를 빼든지, 21a_0 를 빼든지, 31a_0 를 빼든지, ..., 더해서 없애고 싶으면 9a_0 를 더하든지 19a_0 를 더하든지 29a_0 를 더하든지...

단서 1과 2를 동시에 만족하는 것은 39a_0 를 더하는 것이다.

 \begin{aligned}10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1+a_0&=\underbrace{13k}_\text{13의 배수}\\ 10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1+a_0+39a_0&=\underbrace{13k+39a_0}_\text{13의 배수}\\ 10^na_n+10^{n-1}a_{n-1}+\cdots+10a_1+40a_0&=\underbrace{13k+39a_0}_\text{13의 배수}\\ 10\times\underbrace{(10^{n-1}a_n+10^{n-2}a_{n-1}+\cdots+a_1+4a_0)}_\text{1의 자리를 제외한 숫자에서 1의 자릿수의 4배를 더한 수}&=\underbrace{13k+39a_0}_\text{13의 배수}\end{aligned}  

10과 13은 서로소이므로, "1의 자리를 제외한 숫자에서 1의 자릿수의 4배를 더한 수"가 13의 배수가 아니고서는 윗 식이 성립할 수 없다. 그러므로 "1의 자리를 제외한 숫자에서 1의 자릿수의 4배를 더한 수"가 13의 배수인지 확인해서 원래 숫자가 13의 배수인지 확인할 수 있다.

마치며

배수 판별법은 그 자체는 간단하고, 실제로 유용하기 때문에 많이 익혀두고 쓰는 방식이다. 하지만 왜 그렇게 되는지 모른 채로 쓰는 건 마음이 편하지 않으니까, 원래 이렇게까지 증명하려는 게 아니었건만 여기까지 왔다. 이런데 흥미가 매우매우 느껴진다면, 정수론(number theory)에 있는 몇 가지 재미있는 주제로 건너가도 괜찮겠다.

증명이 끝났으니 다음 글에서는 배수 판별법을 모아 정리해 보겠다.