4 ÷ 3과 4 / 3 는 왜 같을까?

분수를 배우고 어느정도 익숙해져가고 있을 무렵, "이제부터는 ÷기호 대신에 분수기호를 쓴다"는 반 주입식 선언과 함께 ÷기호가 교과서에서 점점 사라지는 걸 목도했던 기억이 납니다. '÷'을 '/'로 바꾸어 쓰는 것은 기호를 교체해서 써도 된다는 것 이상의 의미가 있습니다. 우리가 '÷'를 처음 배울때와 '/' 를 배울 때 서로 다른 지점에서 시작했거든요.

 4 \div 3 = \frac{4}{3} 

이제는 너무 익숙해졌겠지만, 하필 저 두 표현식이 같을 필요가 있을까 하는 의문을 억지로 가지고 다시 시작해 봅시다. 4÷3 은

4라는 양을 3명에게 똑같이 나누어주었을 때 한 사람이 얼마나 가지게 되나? 즉 몫(quotient)이 얼마인가?

혹은

4라는 양을 3만큼 똑같이 나누어주면 몇 사람에게 나누어줄 수 있을까?

라는 질문을 식으로 나타낸 것입니다. 나눗셈을 처음 배울 때 그렇게 배웠었죠. 지금 우리가 붙잡고 있는 4÷3 예제에서는 첫번째 질문이 더 자연스러워 보입니다.

 분수 \frac{4}{3} 은

1을 세개로 나눈 한 조각 (즉, \frac{1}{3}) 을 4개 모아 놓은 것

이란 뜻입니다. 분수를 배울 때 저렇게 배웠었죠. 

 4 \div 3과 \frac{4}{3}을 그림으로 나타내면 이렇습니다. 

 4 \div 3은 마치 4에서 시작해서 3등분하면서 양이 줄어든 것 처럼 보이고, \frac{4}{3}은 \frac{1}{3}이란 작은 값이 4배가 되면서 커진 것처럼 보이죠. 그럼 이 두 값은 왜 같은 걸까요?  

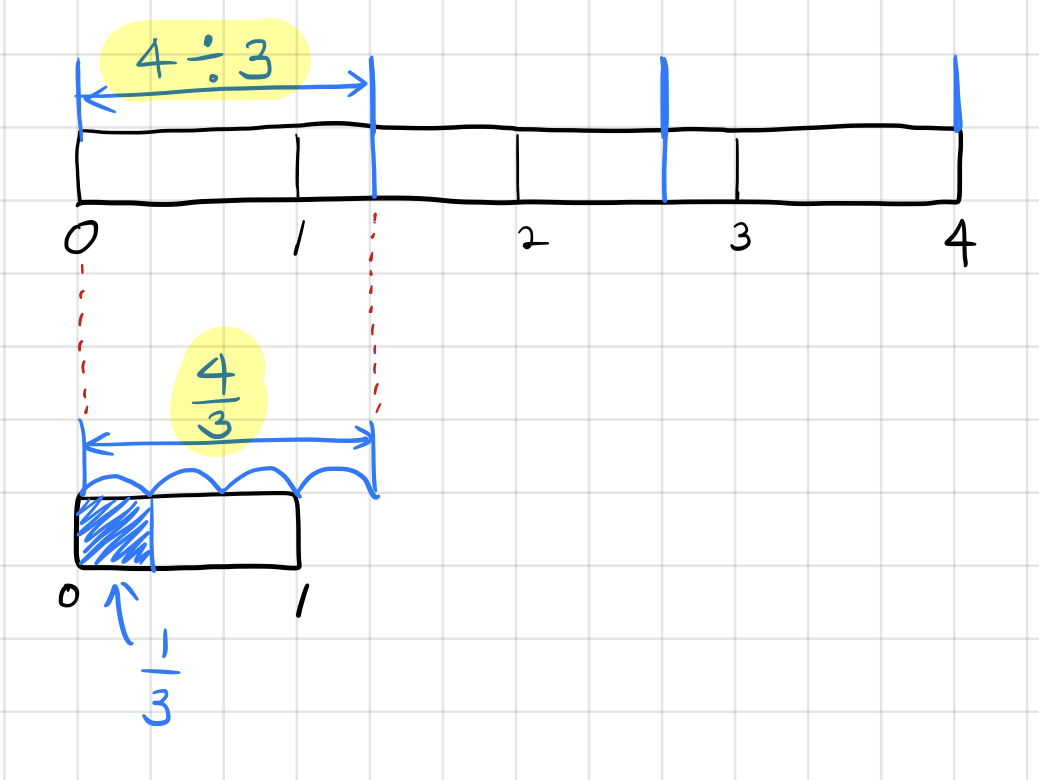
숫자 1에서 시작해 봅시다. 

 1 \div 3 = \frac{1}{3}  

위의 식이 같다는 것은 쉽게 알 수 있을 것 같습니다. 1을 3명에게 정확하게 나누어주면, 각 사람은 1을 3등분한 한 조각을 가지게 될 테니까요. 

이것에 동의했다면, 1의 4배인 4를 나누어준다면 한 사람 몫은 얼마가 될까요? 나누기 전의 값(피제수, dividened)이 정확히 4배가 되었으니, 같은 방법으로 3명에게 나누어준다면 각 사람의 몫도 정확히 4배가 되지 않을까요? 

 4 \div 3 = (4\times1) \div 3=4\times \frac{1}{3}=\frac{4}{3}  

숫자 4, 3에 대해서 4 \div 3=\frac{4}{3}이 납득되기 시작했다면, 다른 자연수에 대해서도 해 봅시다. 모든 자연수에 대해서 비슷한 방식으로 이해할 수 있다는 걸 알게 됩니다.

이것만으로 ÷기호 대신 / 를 사용하는 것이 다 설명되지는 않습니다. 자연수 두 개에 대한 나눗셈 연산에 대해서만 감을 잡아본 것이니까요. 

다음 글에서는 4 \div \frac{1}{3} = 4 \times 3이 왜 되는지 알아보겠습니다. 끝.