분수로 나누면 왜 곱하기가 될까?

이전 시간에 4÷3이 4/3와 왜 같은지 짚어 봤었지요. 이번에는 자연수를 분수로 나누면 왜 곱하기가 되는 지 알아보겠습니다. 예를 들어 4÷ (1/3) = 4 x 3 이 된단 말이죠. 일단은 분자가 1인 분수로 나누는 걸로 시작해서 확장해 보겠습니다.

 4 \div \frac {1}{3} = 4 \times 3 

왜 이렇게 되는 걸까요? 우리가 아는 것만으로 시작해 봅시다. 우린 지금 기본적인 감(intuition)과 이전에 봤던 \text{(자연수)} \div \text{(자연수})=\frac{\text{(자연수)}}{\text{(자연수)}}이 된다는 지식만 가지고 있는 상태죠.

1을 기준으로 시작해 봅시다

이번에도 1을 기준으로 시작해서 확장하는 것이 편합니다.

 1 \div \frac{1}{3} = 3 

 이것부터 납득해 봅시다. 우리가 나눗셈을 처음 배울 때를 떠 올려 보면 위의 나눗셈은 기본적으로 아래 두 가지 상황을 나타냅니다.

1 을 \frac{1}{3} 사람에게 나누어 주면 한 사람이 받는 양(즉, 몫, quotient)은 얼마일까?

혹은 

1을 똑같이 \frac{1}{3}만큼 나누어준다면 몇 사람한테 나누어줄 수 있을까?

둘 중에 어느 표현이 편한가요? (혹은 마음이 덜 불편한가요?) 아래쪽 표현이지요. 사람이  \frac{1}{3}  명이 있다는 건 무언가 어색하니까요. 

그러니 아래쪽 표현을 가지고 접근해 봅시다. 굉장히 직관적으로 답이 3이란 걸 알 수 있습니다. 1이라는 한 덩어리를 각 사람마다 똑같이 \frac{1}{3} 조각씩 나누어 준다면 당연히 3명한테 딱 떨어지게 나누어 줄 수 있겠죠.

이제 원래 양이 1이 아니라 그것의 4배인 4를 나누어 준다면, 1을 나누어 줄 때 3명에게 줄 수 있었으니, 그것의 4배인 12명에게 나누어 줄 수 있지 않을까요? 그래서

 4 \div \frac {1}{3} = 4 \times 3  

이라는 식이 성립합니다. 

그림으로도 알 수 있죠

숫자선(number line)을 이용해서 한 번 나타내 보겠습니다. 우리가 수를 이해하는 데 있어서

분모 혹은 진법(십진법, 2진법, 8진법 등)은 양을 재는 데 쓰이는 보조 눈금

이라고 생각하면 많은 경우(느낌상으론 거의 모든 경우) 맞습니다.

숫자선을 그리면서 우리가 관심있는 분수의 분모가 3이니까, \frac{1}{3} 마다 보조눈금을 찍어 줍시다. 그러니까 가장 작은 눈금 한 칸은 이제 \frac{1}{3} 입니다.

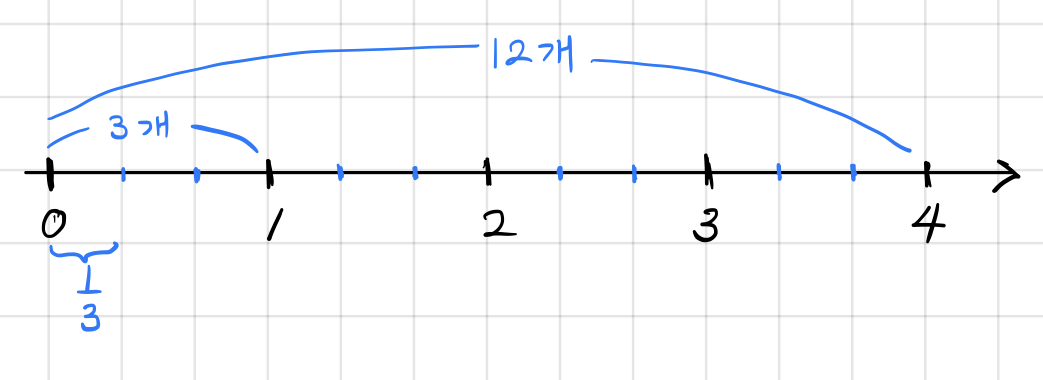
확연히 보이죠? 한 사람마다 \frac{1}{3} 씩 나누어주기로 한다면, 1 안에는 \frac{1}{3} 이 3개가 쏙 들어가니 3명에게 나누어 줄 수 있는 것이고, 4 안에는 \frac{1}{3} 이 총 12개 들어가니 12사람에게 나누어 줄 수 있게 됩니다.

이것은 3, 4 이외에도 일반적으로 성립하는 것이고요. 몇 개 다른 숫자에 대해서 해 보면 자연수라면 다 된다는 것을 알 수 있습니다. 그래서 자연수 a, b에 대해서

 a \div \frac{1}{b}=a \times b  

 \frac{2}{3} 같은 걸 나누면 어떻게 되나요?

흠.. 두 가지 방법으로 접근해 보겠습니다. 한 가지 방법은 우리가 지금까지 알고 있는 것으로 머리가 조금 아파도 접근해 보는 것이고 다른 하나는 이것을 이해할 수 있는 다른 모형을 들고 올 겁니다. 

새로운 모형?

다른 모형을 들고 오는 건 다음 글이나 다다음 글에서 해 볼게요. 다만, 다른 모형을 들고 와야 하는 이유를 잠시 짚어 보겠습니다. 

앞에서도 재차 사용했었지만 우리가 나눗셈 a ÷ b 을 배웠을 때, 두 가지 모형을 배웠고, 둘 중 편한 것을 사용해 왔습니다.

a라는 양을 "b 명"에게 나누어 주면 한 사람당 얼마씩 받게 되나? 즉 몫이 얼마인가?

혹은

a라는 양을 한 사람당 b씩 나누어주면 "몇 명"에게 나누어줄 수 있나?

그런데 이 두 모형은 치명적인 약점이 있습니다. 첫번째 모형에서는 나누는 수(제수, divisor) b가 자연수가 되어야 이해가 편하고요, 두 번째 모형은 나눗셈의 결과가 자연수가 되어야 머리가 편합니다. 그런데 \frac{2}{3}  같은 걸로 나누면 나누는 수가 이미 자연수가 아닌 분수이고, 그 결과 또한 자연수가 아닌 경우가 생겨버려서 불편한(체한 것 같은, 뒷목을 숟가락으로 긁는 듯한) 느낌이 들죠.

아, 그럼 우리가 지금까지 알고 있는 모형이 잘못된 건가요?

그런 건 아닙니다. 우리가 다룰 나눗셈이라는 연산, 분수라는 표현식은 우리의 생각보다도 훨씬 더 유용한 것이고, 마치 만능 열쇄(master key)같은 거라서 앞 문(자연수)를 열 때에도, 뒷문(정수)이나 옆문(분수)를 열 때에도 쓸 수 있는 건데, 지금까지 앞문만 죽어라 열고 있었던 거죠. 앞문 말고 다른 문도 열리는지 해 보면 됩니다.

하지만 이번 글에서는 새로운 모형 대신, 조금 불편하더라도 지금 아는 것만 가지고 해 보죠.

알고있는 것만으로 해 봅시다

 1 \div \frac{2}{3}=\frac{3}{2} 

 이것부터 왜 되는지 알아보죠. 이것을 위해서 2 \div \frac{2}{3} 을 먼저 알아볼 겁니다. 2라는 양을 \frac{2}{3} 씩 나누어 주면 몇 명에게 돌아갈까요?

우리가 관심을 두는 분수의 분모가 3이죠? 3을 보조눈금으로 해서 2까지 숫자선을 그려봅시다. 그리고 그 안에 \frac {2}{3} 가 (즉 \frac{1}{3} 이라는 눈금 2칸을 한 덩어리로 보면) 몇 개 들어가나요? 정확하게 3개 들어갑니다. 

즉, 2 \div \frac{2}{3} = 3 이죠

2를 \frac{2}{3} 씩 몫으로 주어 나누었을 때 3사람에게 정확하게 돌아갔다면, 그것의 절반인 1을 같은 방식으로 나누어주면,  3사람의 절반인 3÷2 즉 \frac{3}{2} 사람에게 돌아가지 않을까요? (한 사람도 두 사람도 아닌 어중간한 한 사람 반이라는 것이 존재한다면 말이죠.) 아직까지 우리는 자연수라는 개념에 갇혀 있으니 약간 마음이 불편한 것은 감수합시다. 

1까지 그린 숫자선을 확대해서 보아도 답이 \frac{3}{2} 라는 걸 알 수 있습니다. 한 번 볼까요? 1 안에 \frac{2}{3} 가 몇 번 들어가나요? 

1번은 들어가지만, 2번까지는 안 들어가고 일부만 들어가죠. 보조 눈금 2칸을 한 덩어리로 보고 있으니 1개는 들어가고, 2번째 덩어리의 반만 들어갔다고 볼 수 있겠네요. 

분수의 덧셈을 배웠다고 가정하면 (지금 분수의 나눗셈을 배우고 있으니 알고 있다고 가정해도 되겠지요) 1 + \frac12 = \frac32 역시 같은 답을 얻을 수 있습니다. 

이것은, 2, 3 말고 다른 숫자에 대해서도 다 적용됩니다. 예를 들어

 1 \div \frac{7}{4}  

의 답을 구하고 싶으면, 숫자선을 1에서 7까지 그린 후, 보조 눈금으로 \frac{1}{4} 마다 점을 찍어 줍니다. 그럼 보조 눈금이 정확히 28개 생깁니다(이게 포인트에요). \frac{7}{4}  은 보조 눈금 7칸을 한 덩어리로 생각하는 것이니, 28개 중에서 7칸씩 배분하면 4명한테 정확하게 돌아가겠죠. 이것을 통해서 7을 \frac{7}{4} 로 나누면 4가 나온다는 것을 알게 됩니다. 그럼 시작이 7이 아니라 그것을 7로 나눈 값인 1로 시작했다면, 4명한테 돌아가던 것이 \frac{4}{7} 명에게 돌아가겠지요. 

그래서 1 \div \frac{7}{4} = \frac {4}{7} 

몇 번 해 보면 자연수가 분자 및 분모인 어떤 분수를 가져 오더라도 1 나누기 그 분수를 하면,  분모, 분자를 바꾼 값이 결과가 된다는 것을 알게 됩니다.

자, 지금까지 자연수 모형에 갇혀서 좀 불편한 가운데 숫자선과 몇 가지 트릭을 동원해서 결과가 어떻게 나오는 지 알아 보았습니다. 

우리 머리를 편하게 해 줄 새 모형을 가져오기 전에 다음 글에서는 (분수) \times (분수) 를 좀 이해해 보겠습니다. (덕분에 새 모형은 다다음 글이 되겠네요) 왜 분자는 분자끼리 곱하고 분모는 분모끼리 곱할까요? 그렇게 쓰고는 있지만 왜 그런지 그려본 적은 아마 별로 없을 거에요. 그럼 이만. 끝