분수의 곱셈을 하기에 앞서서 분수를 1보다 작은 보조눈금으로 이해하는 것을 해 보겠습니다. 이야기가 약간 산으로 갔다가 다시 돌아왔다는 것은 비밀.
분수의 곱셈에 대해서 본격적으로 이야기 하기 전에, 우선 분수를 어떤 개념으로 볼 수 있는지 되짚어보겠습니다. 이전 글에서도 한 번 언급했었지만
분수(특별히 분모)와 진법은 무언가를 재기 위한 단위 혹은 눈금
이라고 생각하면 많은 경우(경험상 거의 모든 경우)에 들어맞습니다. 우리가 길이를 잴 때, 센티미터(cm)로 된 자(ruler)를 쓰기도 하고 인치(inch)로 된 것을 쓰기도 하고, 좀 큰 것을 재어야 할 때에는 미터(meter)나 피트(feet)를 사용하는 것처럼, 같은 길이 혹은 크기를 나타낼 수 있는 표현 방식이 여러가지로 존재합니다. 그리고 서로 다른 단위 사이를 자유롭게 변환해 가며 사용하고 있죠.
321cm라는 길이가 있다고 합시다. 우리는 이것을 3m 21cm이라고도 쓰고, 321cm이라고도 쓰죠. 1m가 1cm 100개랑 같다는 것을 알고 있고, 이들 사이의 변환을 자유롭게 하고 있는 겁니다. 우리가 생각보다 똑똑하죠.
그럼 321이라는 숫자 그 자체는 어떨까요? 수(number)라는 것이 역사가 오래되어서 단정할 수는 없지만, 사람 손가락은 보통 10개이기 때문에, 세다가 10이 넘어가면 기억하기가 애매해서 10개가 넘을 때마다 그걸 하나로 묶어서 다른 단위로 표현하는 방식이 생겨났다고 보는 것이 주류 견해입니다. 하나씩 세다가 10개가 되면 그것을 십(ten)이라는 새로운 단위(혹은 새 이름, 새 묶음)로 묶어서 표현하고, 십이 10번 모이면 백(hundrend)라는 새 단위로 표현합니다. 이것을 십진법(decimal system)이라고 합니다.
다시 321이라는 숫자를 보면, 이 숫자는 백이 3개, 십이 2개, 일이 1개 모인 숫자로 가장 간단하게 이해할 수 있습니다. 하지만 우리가 앞에서 m와 cm단위 사이를 자유롭게 바꾸어서 생각할 수 있었듯이, 이 똑같은 숫자를
십이 32개 일이 1개
백이 3개, 일이 21개
백이 2개 십이 12개 일이 1개
일이 321개
등등으로 생각할 수 있고, 실제로 그렇게 사용하고 있습니다. 언제 사용하느냐? 예를 들어 23에서 8을 뺀다고 해 봅시다. 우리가 전략적으로는 "3에서 8을 뺄 수가 없으니 앞자리에서 10을 빌려와서 뺀다"는 식의 방법들을 익혀서 사용하고 있습니다만, 실제로는 23이라는 숫자를 "십이 2개 일이 3개"로만 인식하는 것이 아니라 "십이 1개 일이 13개"인 것으로 바꾸어 생각할 수 있기 때문에 그런 전략을 만들어 낼 수 있었던 것이죠.
다시 3m21cm의 예제로 돌아가 봅시다. 여기에서 30cm을 빼려면 어떻게 할까요? 미터(m) 3개와 센티미터(cm) 21개로 나타나는 길이를, 미터(m) 2개와 센티미터(cm) 121개인 것으로 재빠르게 전환한 다음 30cm을 뺍니다. 이렇듯 여러 단위로 표현된 측정치에 대한 연산을 할 때이든, 순수한 숫자에 대한 연산을 할 때이든, 우리는 같은 개념을 적용하고 있는 겁니다.
이제 이런 숫자를 어떻게 쓰는 것이 좋을까요? 우선 어떻게 소리내어 읽었는지부터 보겠습니다.
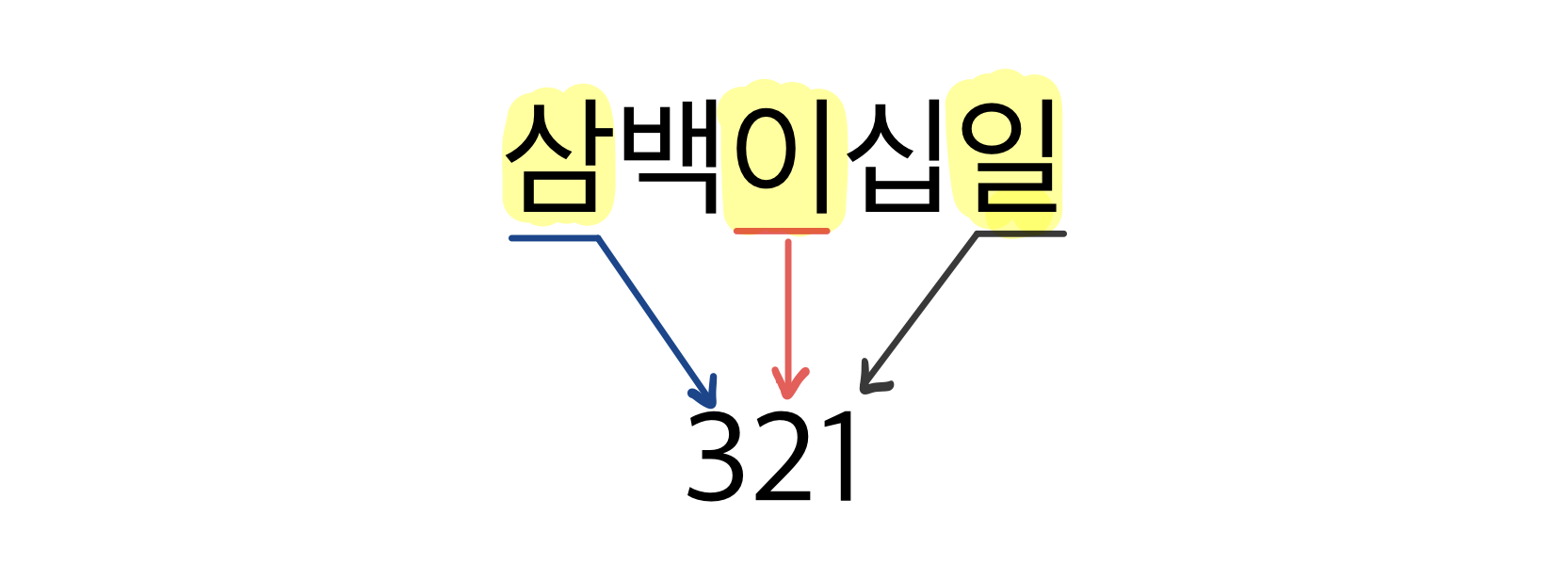
백이 3개, 십이 2개, 일이 1개인 숫자를
삼백이십일
이라고 줄여서 읽습니다. 그런데 여기서 문제가 하나 있습니다. 10개가 넘어갈 때마다 단위를 만들어야 하는데, 그 때마다 새로운 이름을 붙여 읽어야 한다는 것이죠. 예를 들어 백이 10번이 되면 천, 천이 10번 모이면 만, ... 이런 식으로 새 이름이 필요합니다. 외워야 할 이름이 너무 많아지겠죠. 물론 중간에 십, 백, 천을 반복해서 덧붙이면서(이름 재활용) 필요한 이름의 갯수를 줄일 수 있습니다만(십만, 백만, 등등), 외어야 할 이름이 많아지는 것을 막을 수는 없습니다.
실제로 이름이 이렇게 많습니다. 십, 백, 천, 만, ..., 억, 조, 경, 해, 자, 양, 구, 간, 정, 재, 극, 항아사, 아승기, 나유타, 불가사의, 무량대수. 문제는 이것 가지고도 표현이 안 되는 숫자가 더 있고, 이름을 또 지어야 한다는 것이죠.
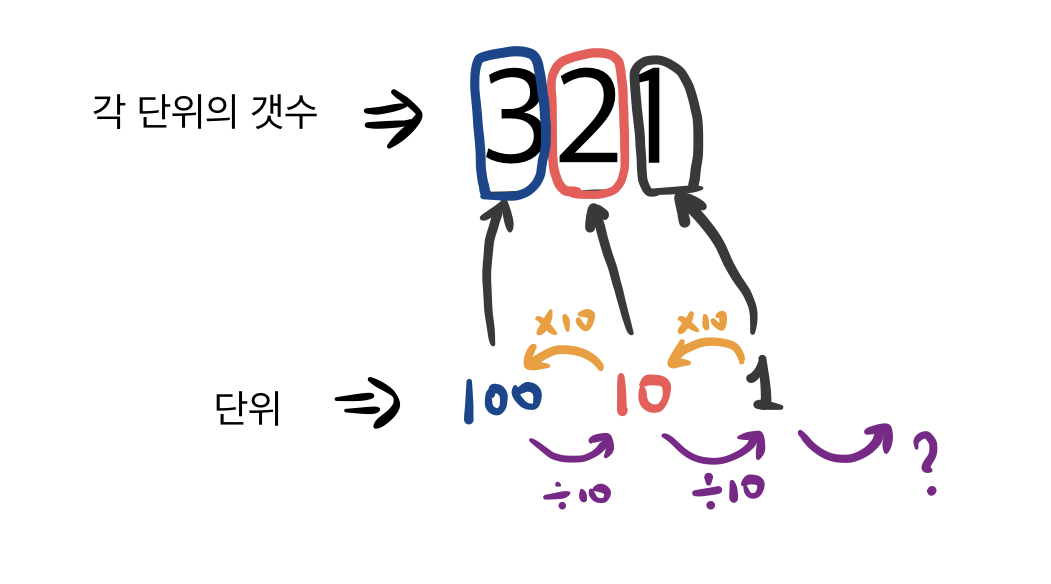
그래서 새 단위마다 이름을 새로 짓는대신에, 위치만 가지고 단위을 표현하는 방법을 도입합니다.
이제 백, 십과 같은 단위는 사라지고, 그 대신 위치만 가지고 표현이 되었습니다. 10개를 모은 더 큰 단위가 필요하면 기존 단위의 왼쪽에다가 그 묶음이 몇개 있는지 숫자로 표시해 놓으면 됩니다. 이 방식을 위치 기수법(Positional Notation)이라고 합니다. 더 이상 10씩 묵어낼 때마다 이름을 외울 필요도, 새 이름을 만들 필요도 없어졌습니다.
하지만 언어는 습관이라서 현대의 우리들은 숫자를 쓸 때에는 위치기수법으로 쓰고, 읽을 때에는 위치기수법에 충실한 방식과 아닌 방식을 섞어서 읽습니다. 무슨 말이냐 하면요.
321은 "십진수 삼이일" 이라고 읽거나, 통상 대부분의 숫자가 십진수이기 때문에 그냥 "삼이일" 이라고 읽는 것이 위치기수법에 충실하게 읽는 방식입니다. 하지만 그렇게 읽지 않고 "삼백이십일"이라고 꼭 백, 십, 일의 단위를 붙여서 읽죠.
그런데, 반대로 작은 숫자는 위치기수법에 충실하게 읽습니다. 0.123 을 한 번 볼까요? 이건 위치 기수법에 충실하게, "영 점 일이삼" 이라고 읽지요. 하지만 옛날에는 소수점 이하 자리마다 그 작은 단위(묶음)을 나타내는 이름이 있었고 그에 따라 읽기도 했습니다.
"일할 이푼 오리" 라고 읽었지요.
지금은 야구 좋아하는 사람이 아니면 모르는 방식입니다. 잘 쓰지 않아서인지 아니면 일본에서 유래해서 그런 것인지 교과서에서도 사라졌거든요.
미국에서는 작은 숫자를 읽을 때 편의에 따라 위치기수법에 충실하게 읽기도 하고 안 그러기도 합니다. 0.24를 어떻게 읽냐고 했더니 point twenty-four hundredths라고 읽더군요. "쩜 백분의 이십사"라는 뜻인데, 좀 괴이하게 읽는다는 생각이 들어서, 0.234는 어쪄냐고 했더니 two hundred thirty-four thousandths라고.. 그래서 옳다구나 해서 0.2345는 어쩌냐고 했더니 point two three four five 라고 하더군요. 별로 일관성은 없는 것 같습니다.
아무튼 한국에서는 321.123을 점 기준으로 왼쪽은 옛날 방식대로(삼백이십일) 읽고, 오른쪽은 위치기수법에 충실하게(일이삼)으로 읽습니다. 전혀 일관성이 없어 보이지만 언어는 관습이니 그려려니 해야겠지요.
숫자를 쓰는데 있어서 위치기수법은 대단한 혁명이었습니다. 우리가 지금은 이미 익숙해져서 이렇게 쓰지 않는 것을 어색하게 여기지만 사실 위치기수법은 전혀 직관적이지 않습니다. 숫자를 처음 배울 때를 기억해 보면, 백은 100이라고 하고, 일은 1이라고 하면서 어째서 백일은 1001이 아니라 101이라고 적는지... 많은 아이들이 헛갈려했었는데, 그 이유는 이것이 혁명적이라서 그런 것입니다. 위치기수법이 도입되기 이전에는 동양에서도 서양에서도 101을 나타낼 때, 백이라는 단위와 일이라는 단위에 해당하는 이름을 정하고 그걸 그냥 이어붙여서 썼습니다. 이렇게요.
한자: 百 + 一 = 百一
로마자: C + I = CI
우리가 위치기수법과 같은 비직관적인 표현을 어렸을 때 이미 받아들여서 아무 문제없이 쓰고 있다는 사실에 약간 자부심을 가져도 되겠습니다.
1의 자리 오른쪽에는 어떤 단위가 와야 할까요? 왼쪽으로 갈 때마다 단위가 10배씩 커지니, 오른쪽으로갈 때에는 10으로 나눈 값을 한 단위로 하는 게 자연스럽습니다. 10개를 묶으면 1이 되는 그 무엇, 바로
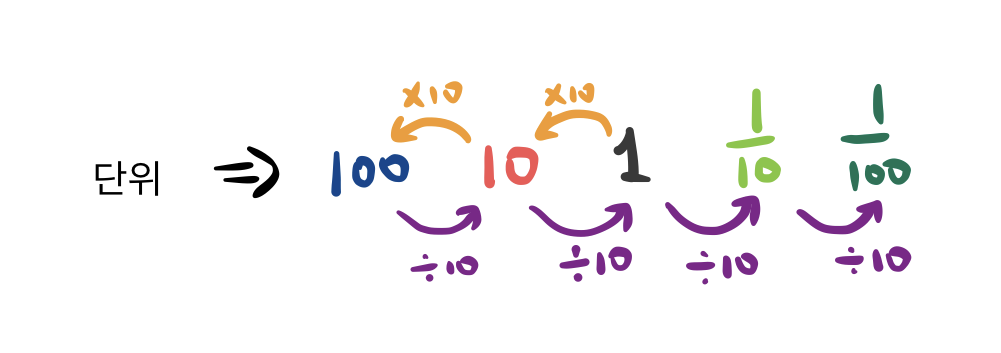
이렇게 우리는 분수를 "작은 단위"라는 개념으로 이미 사용하고 있었습니다. 우리가 사용하고 있는 것이 10진수이기 때문에
예를 1.3이라는 숫자는 1이 1개,
이런 숫자를 수직선에 나타내면 1씩 큰 눈금을 찍고, 그 사이

그런데 1안에 보조눈금을 1/10마다 꼭 찍어야 한다는 법은 없지요. 편의에 따라 덜 세밀해도 상관없으면 1/2마다 찍을 수도 있는 것이고, 1/4마다 찍을 수도 있습니다. 실제로 영미권에서는 1인치(inch) 안에 1/2마다 큰 보조눈금, 1/4마다 작은 보조 눈금, 1/8마다 더 작은 보조 눈금, 1/16마다 진짜 작은 보조눈금을 그어놓고 눈금 갯수 세어가면서 길이를 잽니다. 그리고는 표현하기를
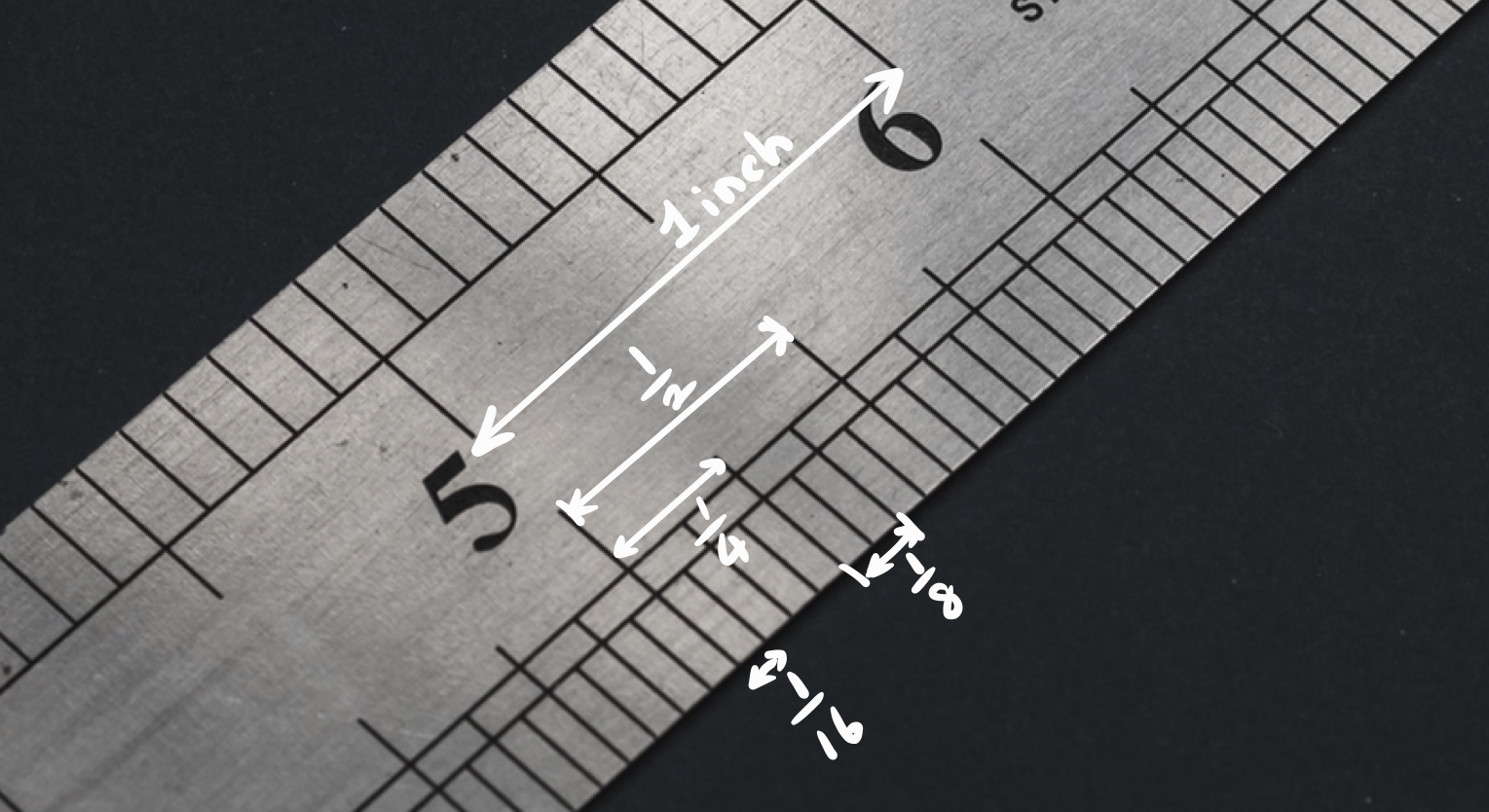
하지만 여기서 무엇보다 중요한 것은
분수라는 것이 1보다 작은 단위(눈금)으로 무언가를 세는 것
이라고 이해하는 것입니다. 이것만 이해하면 그 다음부터는 모든 것이 순조롭습니다.
지금부터 분수의 일반적인 내용들을 눈금 및 단위의 관점에서 이해해 보겠습니다.
1/3과 1/3을 더하면? 1/3이라는 눈금으로 재었을 때, 눈금 한 칸 되는 길이와 또 한칸 되는 길이를 더했으니 눈금 두 칸이겠지요. 그래서 2 개의 1/3, 즉 2/3이 됩니다.
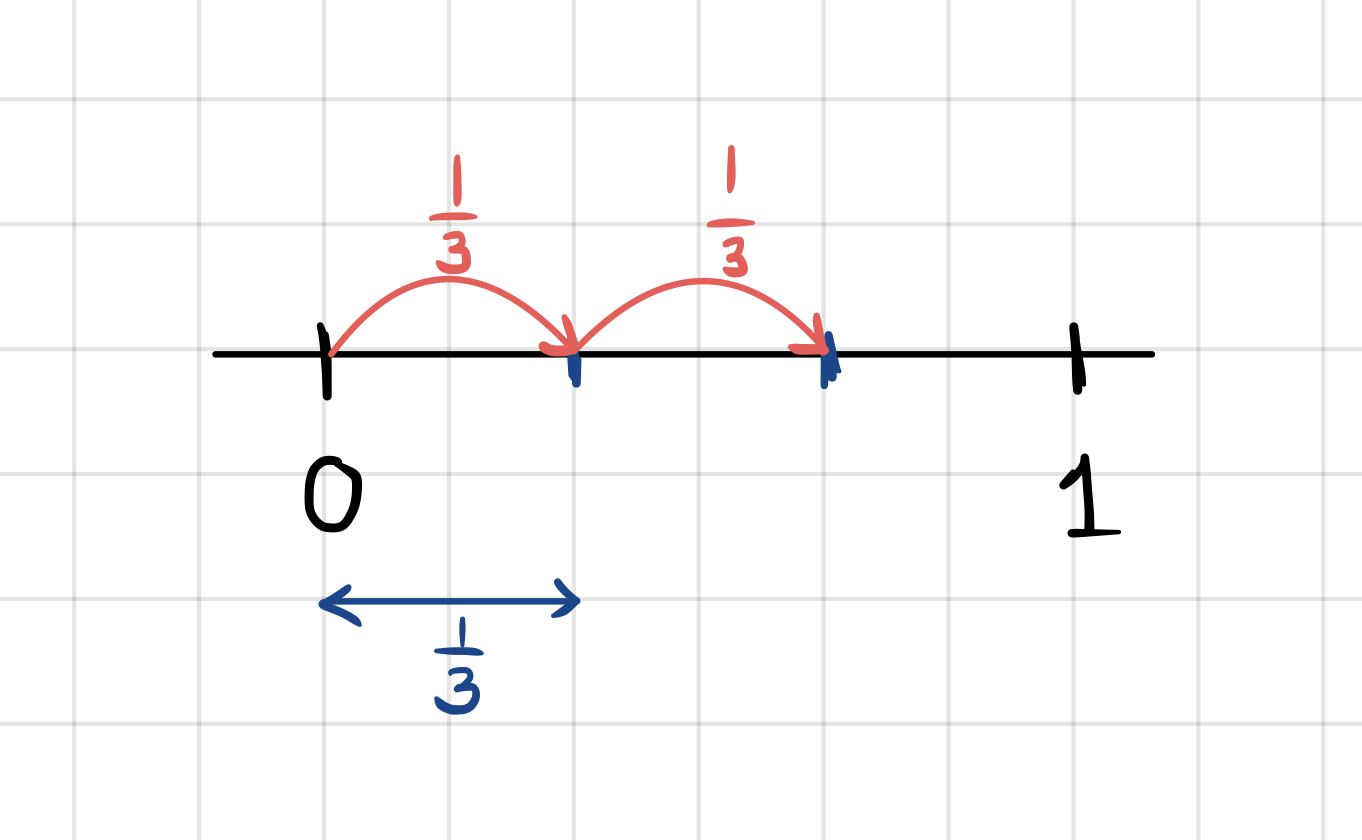
영어로는 더 쉽습니다. 영어로는 1/3을 one third라고 읽는데, third를 마치 미터(m)나 센티미터(cm) 마냥 단위 취급을 해 버리면, 1 third + 1 third = 2 thirds 가 되어서 의심할 여지 없이 2/3 가 됩니다.
약간 억지같지만, 우리말로 풀면서도 영어처럼 "/3"을 마치 단위인 것 처럼 풀어볼 수 있습니다. "나누기 3(삼)"이니까 줄여서 "나삼" 이라고 읽어봅시다. 1/3은 이제부터 1 나삼 입니다.
1 나삼 + 1 나삼 = 2 나삼, 즉 2/3
다른 숫자에 대해서도 동일합니다.
1/4 + 2/4는 1나사 + 2나사 = 3나사, 즉 3/4
3/5 + 7/5 는 3나오 + 7나오 = 10나오, 그런데 10 / 5 = 2 이므로 최종 답은 2
분모가 다르면 어떻게 더할까요? 1/4+ 1/2 처럼요. 두 개가 서로 다른 눈금으로 길이가 재어져 있으니, 바로 더할 수가 없습니다. 마치 2cm + 6inch를 단위 변환 없이 더할 수 없는 것과 같지요. 이럴 때에는 눈금이 같은 자(ruler)로 다시 재어서 더합니다. 1/2이란 길이를 1/4눈금으로 재면 두 칸 나와서 2/4가 되고, 이제 같은 눈금을 가지게 되어서 더할 수 있게 됩니다. 그래서 1/4+ 1/2은 1/4+2/4이 되어서 답이 3/4가 됩니다.
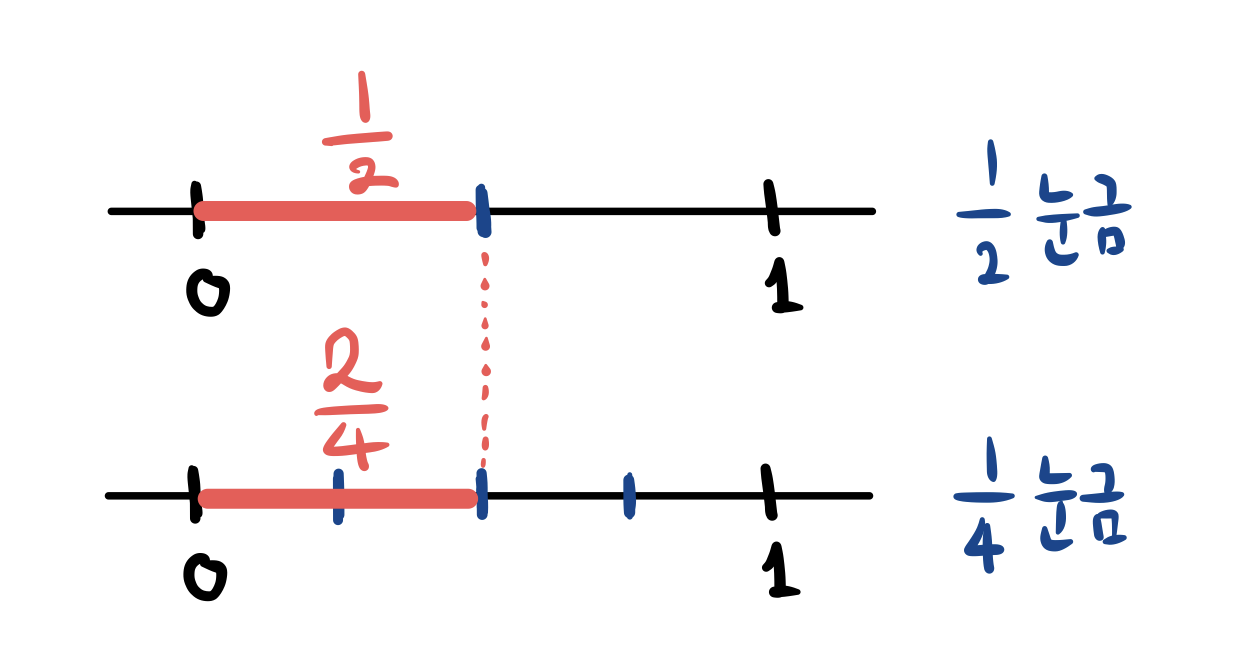
이렇게 같은 눈금자로 재는 것을 통분(reduction to the common denominator)이라고 합니다.
똑같은 길이를 어떤 눈금자로 재느냐에 따라 표현이 달라집니다. 1/2을 1/4눈금으로 재면 2칸 나오니 2/4로 쓸 수 있고, 1/8눈금으로 재면 4칸 나오니 4/8라고도 쓸 수 있지요. 이렇게 눈금따라 다르게 표현되지만 실제로는 같은 분수들을 equivalent fractions(우리말에는 대응되는 적당한 말이 없네요. 같은 분수?)라고 합니다.
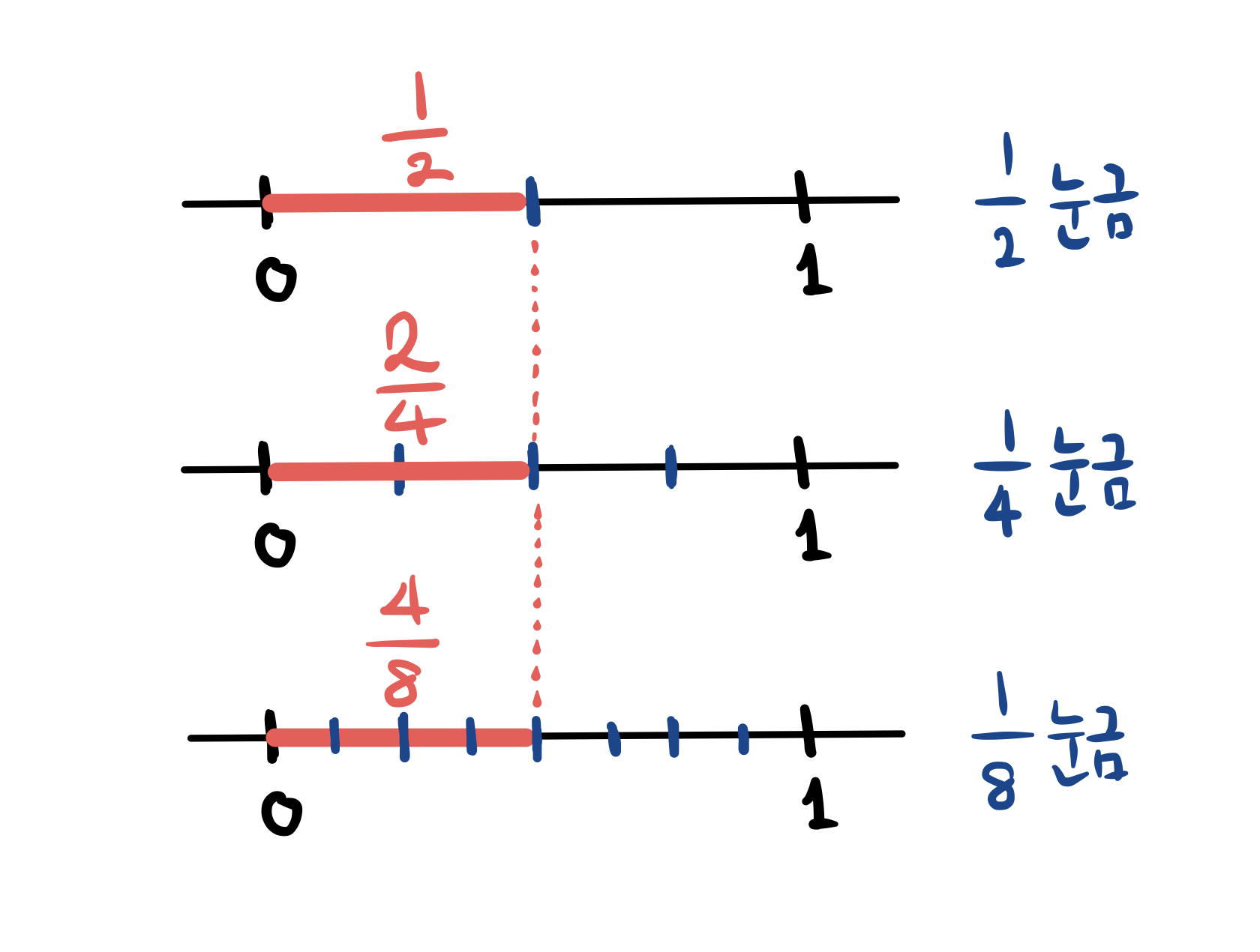
같은 길이를 나타내는 Equivalent fraction중에서 가장 덜 조밀한, 즉 가장 성긴 눈금으로 잰 것을 기약분수(irreducible fraction) 이라 합니다. 위의 예제에서는 1/2이 가장 눈금이 덜 조밀해서 기약분수가 됩니다.
m(미터)라는 큰 눈금과 cm(센티미터)라는 작은 눈금으로 표현된 길이를 한 번 생각해 보겠습니다. 3m 21cm는 321cm으로 나타내기도 하지요. (2m 121cm라고 표현할 수는 있지만 그렇게 잘 안 합니다.)
즉 큰 눈금으로 나타낼 수 있는 만큼 다 나타내고, 큰 눈금으로 표현 안 되는 나머지 부분을 작은 눈금으로 나타낸 것이 3m 21cm 이라는 표현이고요,
큰 눈금으로 나타낼 것이 있음에도 작은 눈금으로만 나타낸 것이 321cm라는 표현입니다.
분수도 마찬가지입니다. 1이라는 큰 눈금과 1을 3등분한 1/3이라는 작은 눈금이 있다고 했을 때,
큰 눈금으로 표현될 부분이 있음에도, 작은 눈금으로만 나타내면 8/3으로 쓸 수 있는데, 이렇게 나타낸 것을 가분수(improper fraction)이라고 합니다.
27cm처럼 큰 눈금 m(미터)로 표현하기는 부자연스러워 작은 눈금으로 표현할 수 밖에 없는 경우가 있지요. 2/3 처럼 아예 크기가 큰 눈금 1이 안 되어서 작은 눈금으로만 표현된 분수를 진분수(proper fraction)이라고 합니다.
2cm의 4배는 8cm죠. 마찬가지로 2/3 (2 thirds) 의 4배는 8/3 (8 thirds) 입니다. 2/3를 하나의 숫자로 보는 게 아니라 2 와 /3로 분리해서 /3을 단위 취급하는 것이 포인트입니다. 앞에서 약간 억지스럽게 만든 "나삼"을 다시 가져와서 읽어보면
이렇게 분수에 자연수를 곱하면 실제로는 분자에 자연수를 곱한 것과 같아집니다. 분모는 보조 눈금(단위)일 뿐이죠.
이제 2/3의 4배는 쉽게 이해할 수 있게 된 것 같습니다. 그렇다면 4의 2/3배는 무엇일까요? 보통은 교환법칙(commutative property)이 성립하므로 2/3의 4배랑 같다고 생각합니다. 하지만 이것은 결론을 어딘가에서 듣고 거꾸로 가고 있는 것입니다. 4의 2/3배를 구해보고 그 값이 2/3의 4배와 같은 것을 눈으로 확인하고 나서 자연수와 분수의 곱셈에 교환법칙이 성립하는 것을 알게 되는 것이지 그 반대로 가면 안 됩니다. 교환 법칙은 특이한 성질이거든요. 고등교과에서 배우는 합성함수나, 행렬곱(matrix multiplication)만 하더라도 교환 법칙이 일반적으로 성립하지 않습니다.
다음 글에서 4의 2/3배를 어떻게 이해할 수 있는지 살펴보겠습니다.
