왜 무한대로 달려야 했을까?

자동차를 타고 목적지까지 50km/h를 유지하면서 달렸습니다. 돌아올 때 좀 빨리 달려서 가고 오는데 평균 100km/h가 되게 하려면 얼마로 달려서 돌아와야 할까요?

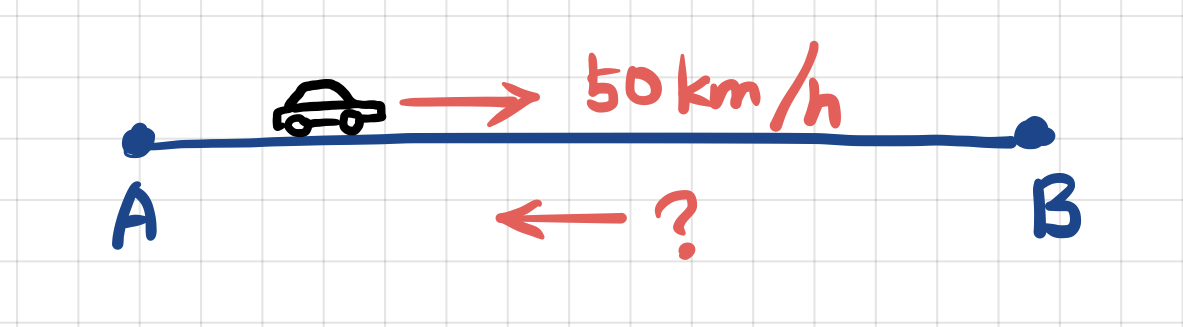
자동차를 타고 A지점에서 출발해서 평균 50km/h의 속도로 목적지 B에 도착했습니다. 되돌아올 때에는 좀 빨리 달려서 평균 100km/h으로 왔다갔다 한 게 되도록 하고 싶다면, 얼마의 속도로 되돌아와야 할까요?

이 글에서는 벡터랑 스칼라를 엄밀히 따지고 있지 않습니다. 그래서 속도와 속력을 혼용하고 있습니다.

대부분의 사람들이 150km/h라고 대답합니다. 예상하시다시피 틀린 답이구요. 평균 속도의 정의가 우리가 생각하는 산술 평균값이 아니라서 그런 것인데요. 평균 속도의 정의를 한 번 볼까요?

 \text{평균속도}=\frac{\text{이동거리}}{\text{걸린시간}}  

흔히 "속도는 거리 나누기 시간" 이라고 하지요. 그것과 정확히 같은 말입니다. 해석이 중요한데요, 평균 속도라는 것은 여러가지 다양한 속도를 다 더해서 평균값을 구한 것이 아니라, 빠르게 가든 느리게 가든, 가다가 중간에 쉬든, 이동한 거리를 구한 다음에 그때까지 걸린 시간을 나눈 것이 평균 속도입니다.

그렇다면 돌아올 때 150km/h로 오면 평균속도가 어떻게 되는 지 한 번 보겠습니다. 평균 100km/h가 아니라는 걸 눈으로 확인해야 속이 좀 시원하겠지요.

출발지점에서 도착지점까지의 거리를 d라고 하면, 이동한 총 거리는 2d입니다. 걸린 시간을 구할 때 "시간은 거리 나누기 속도"이므로, 갈 때 걸린 시간은 d/50, 올 때 걸린 시간은 d/150입니다. 이제 계산해 볼까요?

 v_{average}=\frac{2d}{\frac{d}{50}+\frac{d}{150}}=\frac{2d}{\frac{3d+d}{150}}=\frac{2d}{\frac{4d}{150}}=\frac{2}{\frac{4}{150}}=\frac{2\times150}{4}=75\text{km/h}  

75km/h밖에 안 나오네요. 평균속도가 100km/h가 되려면 돌아올 때 좀 더 빨리 달려야 하나봅니다. 그러면 돌아올 때 300km/h로 달려오면?

 v_{average}=\frac{2d}{\frac{d}{50}+\frac{d}{300}}=\frac{2d}{\frac{6d+d}{300}}=\frac{2d}{\frac{7d}{300}}=\frac{2}{\frac{7}{300}}=\frac{2\times300}{7}\approx85.7\text{km/h}  

그렇게 달려도 평균 85.7km에 밖에 도달을 못하네요. 도대체 얼마로 달려야 할까요?

답은 빛의 속도로 달려도 평균 100km/h에 도달을 못합니다. 무한대로 달려야 해요.

왜 그럴까?

이런 종류의 퍼즐을 대하기 전에 감을 잡는 팁을 잠시 말해 보겠습니다. 

처음에는 속도, 거리, 시간 중에 갈 때의 속도 하나만 알고 있으니(거리도 모르고 시간도 모르고 돌아올때의 속도도 모르고) 아무것도 도출해 낼 수 없을 것 같은 느낌이 들지요. 하지만 생각해 봅시다. 우리가 어떤 속도로 달리든 거리를 바꿀 수는 없잖아요. 그런데 그 거리가 얼마인지 문제에 주어져 있지 않아요. 이것은, 만약에 이걸 해석할 수 있는 방법이 있다면 그것이 거리에 전혀 상관없이 성립할 것이라는 단서를 던져 줍니다. 대수학에 익숙하면 거리를 그냥 d 같은 문자로 놓고 풀면 어느 순간엔가 상쇄(cancel-out)되어서 없어질 것이라는 뜻이죠. 또 다른 의미로는 우리에게 편한 숫자 아무거나 넣고 생각해도 된다는 뜻입니다.

그래서 편한 숫자를 하나 골라서 거리가 100km라고 해 봅시다.

평균 100km/h로 갔다가 돌아오려면, 총 거리는 가고 오고 해서 200km니까, 2시간 안에 갔다가 돌아와야 합니다. 그런데 갈 때 50km/h로 갔으니 가는 데만 2시간이 걸린 거죠. 돌아올 때에는 0시간 안에 돌아와야 합니다. 그래서 순간이동하지 않는 한 평균속도 100km/h에 도달할 수가 없습니다.

평균 속도와 조화 평균

우리에게 익숙한 평균값이라는 것은 주로 산술 평균입니다. 숫자 a, b에 대한 산술평균 m은 a, m, b의 세 숫자가 등차수열을 이루게 만드는 m의 값을 말합니다. 손쉽게 계산하자면 두 숫자 더한 후에 2로 나누면 됩니다. 하지만 이런 평균 이외에도 기하평균(기하수열의 중간값)과 조화평균(조화수열의 중간값)이란 것이 있습니다. 

조화수열이란 역수를 취했을 때 등차수열이 되는 수열입니다. 대표적으로 이런 것인데요,

 \frac{1}{2},\frac13,\frac14,\frac15,\cdots  

위와 같은 수열은 아래위 뒤집으면, 2, 3, 4, 5, \cdots 형태의 등차수열이 되므로 조화수열입니다. 조화평균은 뒤집어서 평균 구한 다음에 그 값을 다시 뒤집은 것입니다.

아까 앞에서 올 때 150km/h로 달리면 평균 속도가 75km/h가 나왔었지요? 같은 거리를 달린 속도의 평균 속도는 조화평균과 같습니다. 조화평균 구하는 방법으로 바로 구해보면, 일단 숫자를 뒤집어서 \frac{1}{50} 과 \frac{1}{150} 의 평균값을 구합니다.

 \frac{\frac{1}{50}+\frac{1}{150}}{2}=\frac{\frac{4}{150}}{2}=\frac{2}{150}=\frac{1}{75}  

그리고 그렇게 구한 값을 뒤집으면 조화평균이 되죠. 75km/h가 딱 나오지 않습니까?

조화(harmonic) 수열이란?

등차수열과 등비수열만 해도 상당히 직관적인데 조화수열은 좀 난데 없는 면이 있습니다. 뒤집으면 등차수열이 되는 수열이라니, 왜 이런 것이 있고, 하필 이름은 조화수열일까요?

이 수열의 시작은 보통 화음이라고들 합니다. 그래서 이름에 "하모니"가 들어간 것이지요.

A장조에서의 "도"(음이름 가, 혹은 A, 계이름은 도)의 진동수가 440Hz라고 할 때, "미"는 550Hz "솔"은 660Hz 입니다. 완전화음이죠. "높은 도"는 880Hz이고요, 그 사이 하나 빈 것같은 770Hz의 자리는 라#(딸림7화음)이 차지하고 있습니다. 그래서 나열해 보면

도, 미, 솔, 라#, 높은 도 ==> 440, 550, 660, 770, 880

110의 차이를 두고 계속 커지는 등차수열입니다. 음악은 옛날부터 있었고 옛날 사람들도 어떤 음이 화음이 되는 지는 알고 있었습니다. 다만 진동수를 측정하는 기술은 그 당시에는 없었겠지요. 파동에서 진동수는 파장의 역수인데, 파장의 길이를 따로 재는 것은 어렵지만, 파동이 특정 공간에 갇혀 있으면(정상파라고 하죠) 파장은 그 갇힌 공간의 길이에 비례하게 됩니다. 어렵게 말했지만 현악기에서 설명하자면 현의 길이와 진동수가 반비례 관계에 있다는 말입니다. 

A장조를 도입한 이유는 4번 A음의 진동수 440Hz가 숫자 계산하기에 좋은데, 이걸 "도"로 시작하는 조를 찾다보니 A장조 기준으로 계이름으로 읽었습니다. 

피타고라스와 그의 추종자들이 역수가 등차수열을 이루는 길이의 현으로 연주하면 화음이 된다는 걸 알아냅니다.(정확하게는 화음을 이루는 현의 길이가 정수비를 이룬다는 걸 알아내는데, 그걸 순서대로 나열해서 역수를 취하면 등차수열이 됩니다) 그리고는 음악에서조차 숫자로 조화로워지는 세상에 감탄하며 정수(integer)를 더욱 더 숭배하게 되었다는... (하지만 오늘날에는 이게 맞지 않다는 걸 압니다. 한 옥타브 안에서 대충 저렇게 맞았다는 것이고요, 실제로 화음이 되는 진동수를 구해보면 등차수열이 아닙니다)

암튼, 결론은 조화수열도 어딘가 쓰인다는 겁니다. 같은 거리를 달린 속도의 평균 속도는 조화평균이란 것과 함께요. (하지만, 같은 시간동안 달린 속도의 평균은 산술평균입니다) 끝