곱셈도 자주하다보면 좀 더 빨리 하는 법이 보입니다. 몇가지 알아볼까요?
제가 초딩 3학년 즈음, 방 안 책장에 꽂혀 있던 특이한 이름의 책 한 권을 발견했습니다.
임
신
법
교
본
아, 우리 아부지는 뭘 이런 걸 내 손이 닿는 데 두셨을까 하고 순수한 호기심에 빼 들었더니 이런 신세계가 있더군요
4자리수 여러개 한꺼번에 더하는 법 (2034 + 1124 + 3024 + ... + 3984 을 한 번에)
곱셈을 문제를 읽으면서 그냥 푸는 법
네.. 종이가 다 누렇게 바랜 "암산법 교본"이라는 옛날 책이었는데, 표지 인쇄가 밀린 건지 제본하다가 밀린 건지 한쪽이 말려들어가서 제목이 그렇게 된 거더군요.
암튼 그 책을 보면서 이것 저것 방법을 익혔던 기억이 납니다. 덧셈을 한꺼번에 하는 것은 합해서 20이 되는 숫자 3개나 4개의 그룹을 통째로 다 외우는 방식었는데, 구구단 외운 지도 얼마 안 되던 터라 고개를 절래절래 했었고요. 뺄셈에 사용되는 10의 보수[(9, 1), (8, 2), ..., (1, 9)] 개념과 9의 보수 [(8, 1), (7, 2), ..., (1, 8)] 개념은 이해도 되고 쓰기 좋아서 계속 썼던 것 같네요.
하지만 무엇보다도 흥미를 끄는 건 곱셈 암산법이었습니다. 십의자리수가 같은 두 자릿수의 암산법. 그 중에서 가장 쉬운 것은 이것이었죠.
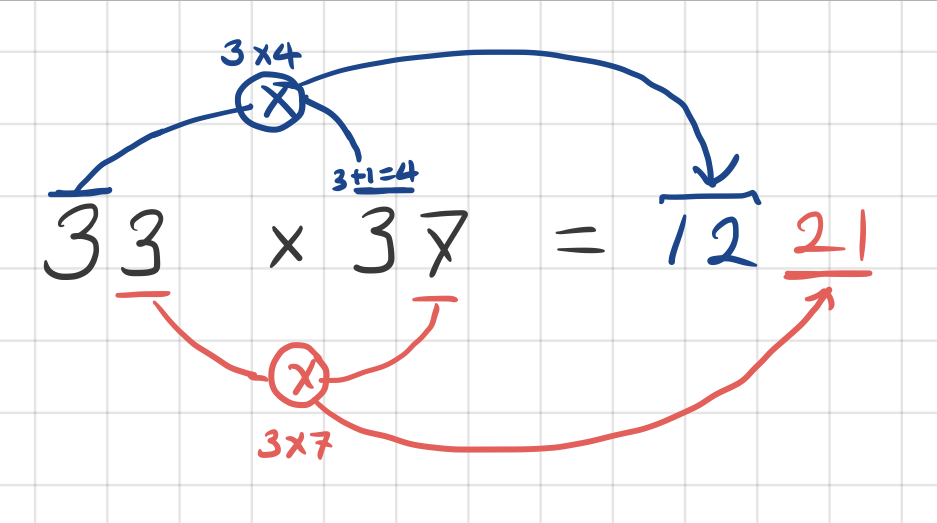
예를 들자면, 24 x 26 같은 겁니다. 85 x 85도 되고요, 33 x 37 도 됩니다.
33 x 37 로 이 곱셈법을 해 보면,
[1단계] 두 숫자의 일의 자리 숫자들을 곱해서 일단 씁니다. 7 x 3 = 21
[2단계] 십의 자리 숫자와 그 숫자에 1을 더한 숫자의 곱을 아까 쓴 21앞에다가 붙여서 씁니다.
3 x 4 = 12이므로 이걸 21앞에 붙이면
1221 끝.
몇몇 숫자에 대해서 실제로 계산해 보면 답이 다 맞다는 걸 알게 될 거에요.
처음에 이 곱셈법을 접하고 신기하기도 하고 약도 올랐던 것 같습니다. 되긴 되는데 왜 되는지 몰랐으니까요. 어떻게든 이유를 알고 싶었는데, 결국 해결을 못하고 일종의 버킷리스트에 올려두었다가 중학교 1학년 즈음에 왜 되는 지 알게 되었죠. 아무리 이해해보려고 해도 문자를 이용한 식을 접하기 전까지는 해결 방법을 알기가 어렵더군요.
그럼 이제 이게 왜 되는 지 봅시다.
두 숫자의 곱셈은 각 숫자를 길이로 하는 직사각형의 넓이를 구하는 것과 같습니다. 그래서 33 x 37은 이렇게 그릴 수 있죠.

33은 30 + 3이고, 37은 30 + 7이므로 이 넓이를 이렇게 4개 조각의 합으로 표현할 수 있습니다.
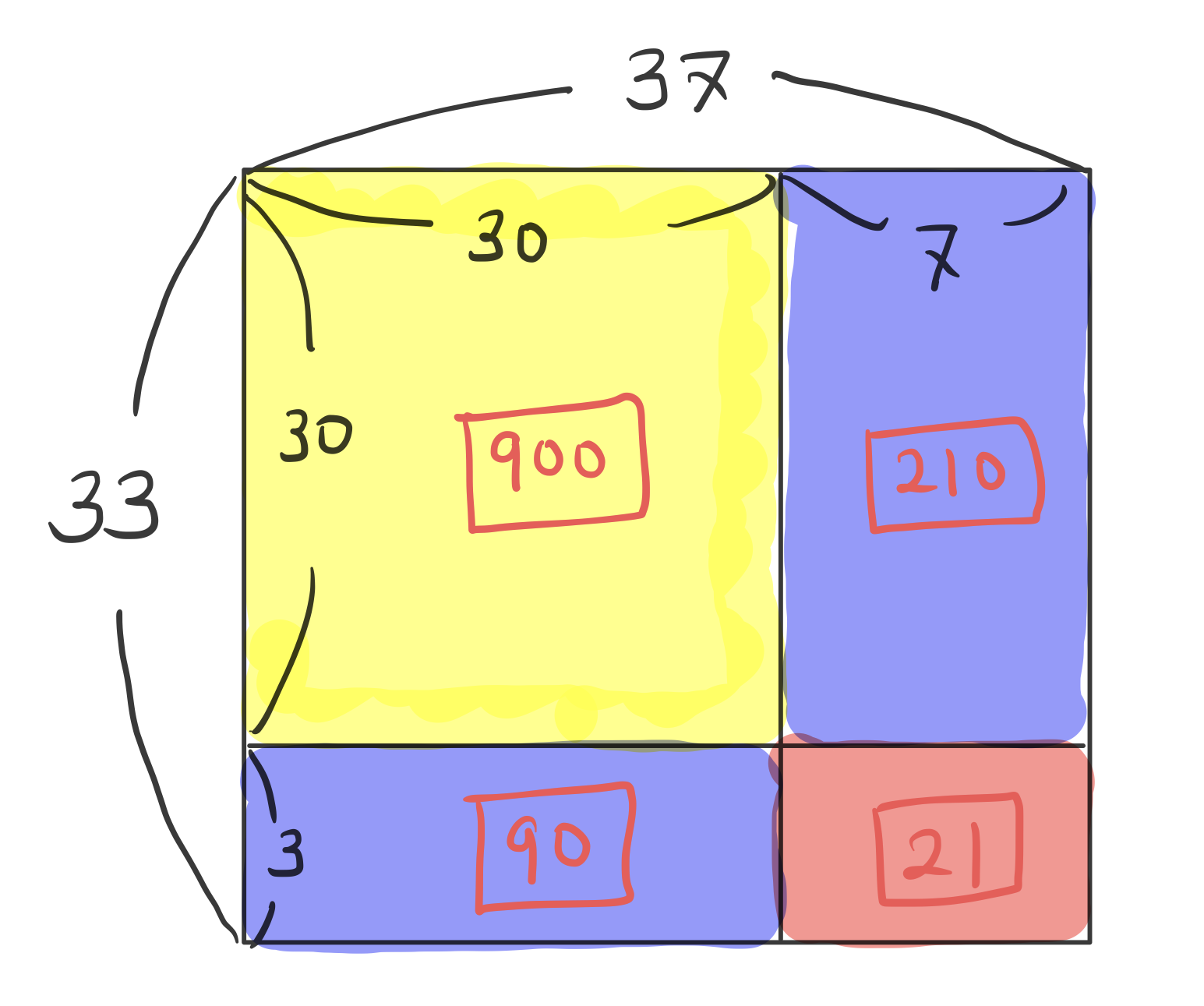
노란 부분은 몇 십(여기서는 30)에다가 몇 십(여기서는 30)을 곱했으니 몇 백(여기서는 900)이 나오는 것이 당연한데요. 재미있는 것은 두 파란 부분입니다. 두 파란 부분을 합치니 210 + 90 = 300 이 되어서 이것 또한 끝자리 두 자리가 0으로 딱 떨어집니다. 그렇기 때문에 최종 답의 끝 두자리는 두 개의 일의 자릿수의 곱인 21이 차지하게 됩니다. 노란부분과 파란 부분은 끝 두 자리가 다 0이니 영향을 안 주거든요. 그리고는 900 + 300 = 1200 이 되어서 이것을 합하면 21 앞에 12을 그냥 붙여 써 놓은 것과 같은 1221이 됩니다.
무언가 감이 오죠? 이제 이걸 일반화 해 보겠습니다.
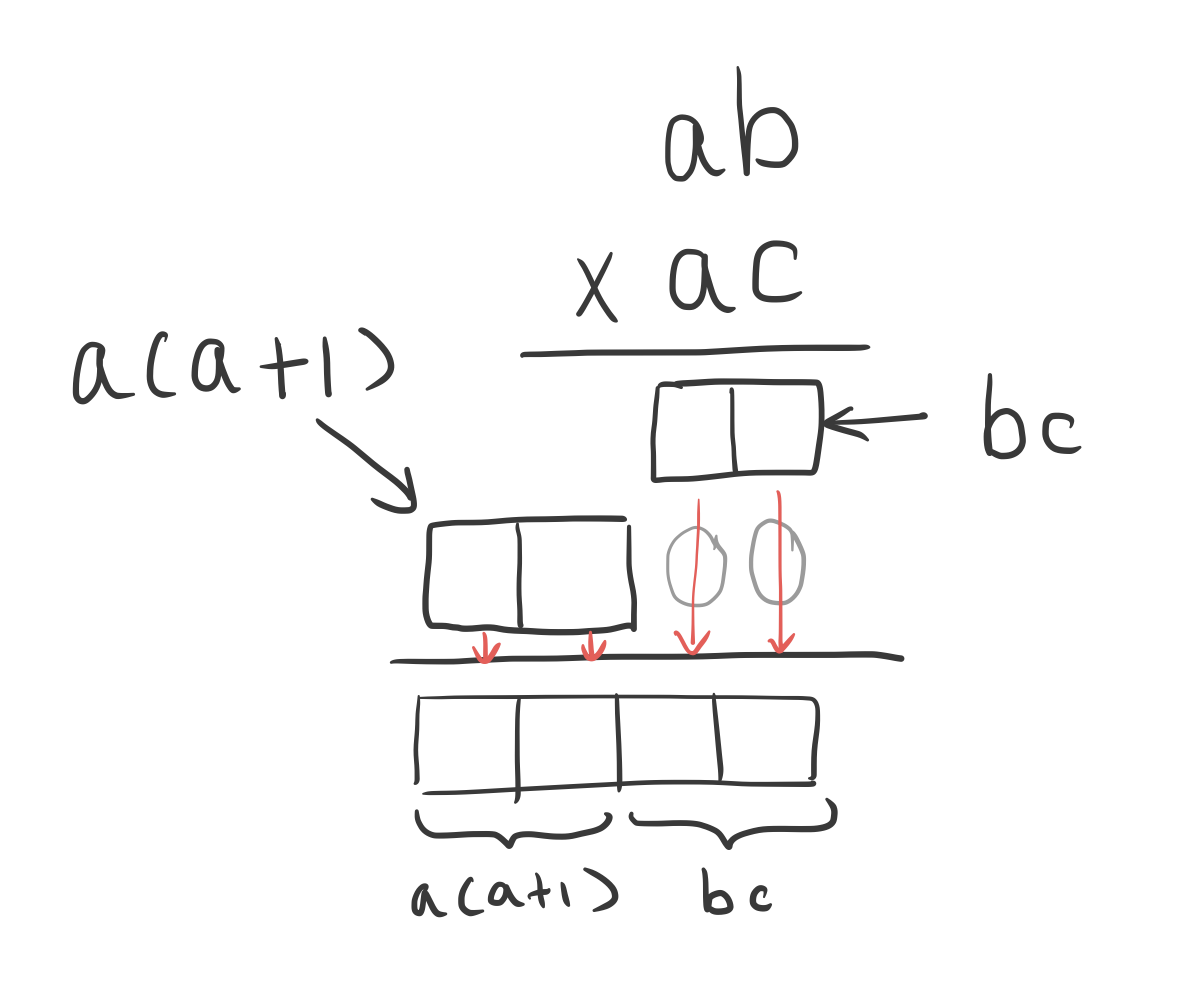
ab라는 숫자와 ac라는 숫자를 곱해 보겠습니다. 단 b+c = 10 이 되겠죠.
이제 같은 그림을 그려보면, ab라는 숫자는 10a + b로 볼 수 있고, ac는 10a + c로 볼 수 있으므로 아래와 같이 그릴 수 있게 됩니다.

여기서도 주목할 부분은 두 파란 부분의 합입니다.
분배법칙으로 10a로 묶어주면, b+c가 10인 경우를 생각하고 있기 때문에 100a가 나옵니다.
노란 부분과 파란 부분을 합하면,
결과값을 해석해 보면 십의 자릿수 a와 그것에 하나 더한 a+1을 곱한 값에 100을 곱했다는 뜻인데요. 이 말은 답이 "몇 백"이니까 백보다 작은 것과 합하면 십의 자리와 일의 자리에 아무 영향을 주지 않는다는 걸 의미하죠.
빨간 부분 bc는 일의 자리 숫자 두 개를 곱한 것이기 때문에 무조건 100보다 작은 어떤 숫자가 나옵니다.(구구단을 생각해 보세요. 100이 넘는 값은 없습니다.) 그래서 최종답의 십의 자리와 일의 자리는 bc에 의해서만 결정되구요, 십의 자리와 그것에 1더한 숫자의 곱은 백의 자리부터 쓰기 때문에 그냥 그 앞에 달아주면 됩니다.
증명 끝.
예를 들어 36 x 37 같은 걸 말합니다. 이걸 계산 할 때에는
[1단계] 일의 자리수를 곱해서 6 x 7 = 42 그 중에 일의자리 숫자인 2는 바로 적고 십의 자리숫자 4는 기억해 둡니다. 여기까지 최종답: 2, 기억해둔 숫자: 4
[2단계] 일의 자리 숫자 합이 10을 초과하는 부분(6 + 7 = 13이므로 3)과 십의 자리 숫자 3를 곱해서 아까 기억해 두었던 숫자 4과 더합니다 (9 + 4 = 13) 그 중의 일의 자리 숫자 3을 최종답의 십의 자리에 적고 십의 자리숫자 1은 기억해 둡니다. 여기까지 최종답 32, 기억해둔 숫자 1
[3단계] 십의 자리 숫자와 십의 자리숫자보다 하나 큰 수를 곱한 것 (3 x 4 = 12)와 아까 기억해둔 숫자 1을 더해서 앞에 달아줍니다. 최종답 1332
좀 복잡해보이지만 익숙해지면, 한 줄에 답이 나옵니다. 원래 암산법에서 나온 거니까요.
ab와 ac의 곱으로 보는 것까지는 똑같고 b + c > 10 이라는 것만 다릅니다.

두 파란 부분을 합하면 같은 방법으로 10a(b + c)가 나오는데요. b+c 부분에 주목해 봅시다. b + c가 10보다 큰 경우를 가정했는데, 0~9까지의 숫자 두 개를 합해서 18보다 큰 경우는 없기 때문에 항상 b + c는 "십몇"이 됩니다. 간단하게 "십몇"을 10(십) + m(몇) 이라고 써 볼까요.
이제 그림이 보이죠. 노란부분, 파란 부분, 빨간 부분을 다 합하면
으로 정리가 되는데요. 앞에서 다룬 "십의자리숫자는 같고 일의자리합은 10이 되는 경우"와 비교해 보면, 다른 건 다 똑같은데 10am이라는 부분이 추가된 겁니다. 10am은 무엇이냐? a는 10의 자리의 숫자였고, m은 일의 자릿수를 합했을 때 10을 초과하는 부분이었죠. 여기에 10을 곱한다는 것은 최종 답을 적을 때 마지막 한칸은 비우고 십의 자리부터 써 준다는 뜻이지요.
100a(a+1)과 10am 그리고 bc를 합하는 과정을 33 x 37을 예제삼아서 써 주면 이렇게 됩니다. 각 부분 계산의 결과값의 자리가 서로 겹치기 때문에 일의 자리부터 써주고, 십의 자리는 기억해 두었다가 2단계 계산 끝나면 그것과 합쳐두고, 다시 백의 자리는 기억해 두었다가 3단계 결과값과 더해주는 것이랍니다.
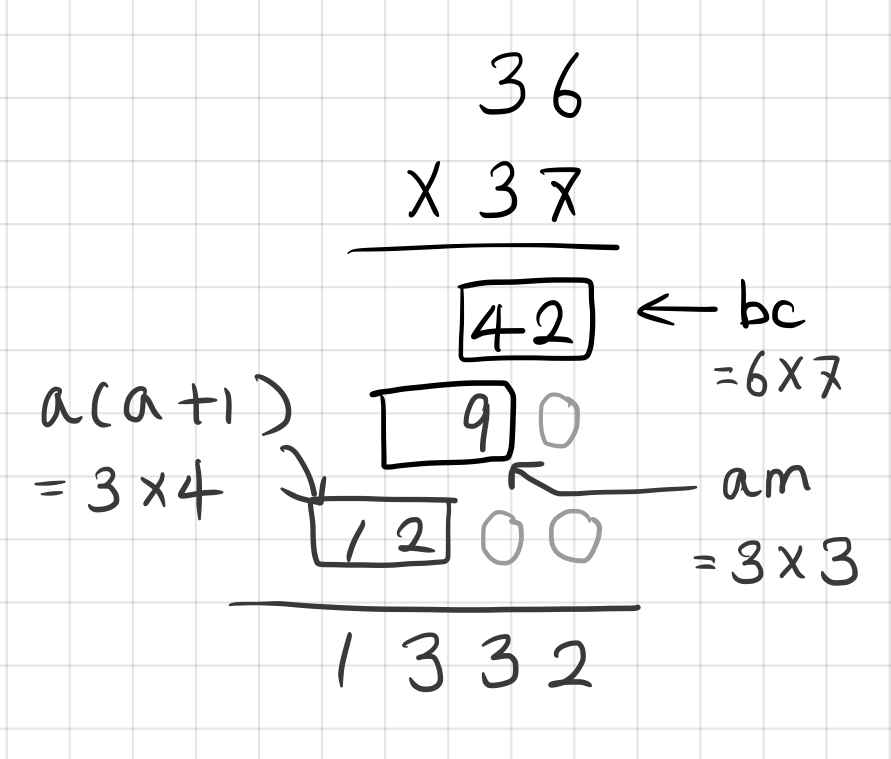
좀 복잡하지만 익숙해지면 한 줄짜리 계산입니다.
33 x 34 와 같은 거죠. 이 예제로 한 번 해 보면,
[1단계] 일의 자릿수끼리곱해서(3 x 4 = 12) 나온 답의 일의 자리숫자(2)는 최종 답에 바로 적어주고 십의 자리숫자(1)는 기억해 둡니다. 여기까지 최종답: 2, 기억해둔 숫자: 1
[2단계] 일의자릿수끼리 더한 값(3 + 4 = 7)을 십의 자릿수 3과 곱해서 (7 x 3 = 21), 아까 기억해둔 숫자 1과 더한 후(21 + 1 = 22), 일의 자리숫자는 바로 최종 답의 십의 자리에 적어주고, 십의자릿수(2)는 기억해 둡니다.. 여기까지 최종답: 22, 기억해둔 숫자:2
[3단계] 십의 자리숫자의 제곱(3 x 3 = 9)에 아까 기억해둔 숫자를 더해서(9 + 2 = 11) 최종 답의 앞에 달아 줍니다. 최종답: 1122
그림도 같고 식도 비슷합니다.

여기서도 주목할 부분은 두 파란 영역이고요. 10a(b + c)가 되는데, b+c가 10보다 작은 경우를 생각하고 있으니 b+c는 항상 한 자리 숫자가 되겠네요. 그냥 m(몇)이라고 해 봅시다.
이제 노란부분 빨간 부분이랑 다 합해보면
이제 익숙해졌으니 각 부분이 의미하는 바는 짐작이 가지요?
10am은 일의자리 숫자끼리의 합인 m에다가 십의 자리 숫자를 곱한 다음 10을 곱했다는 뜻입니다. 즉 일의 자리 숫자끼리의 합에 십의 자리 숫자를 곱한 값을 최종 답의 10의 자리부터 써 준다는 뜻이죠.
이 세 가지 부분 계산의 합을 33 x 34 의 예를 기준으로 적어주면 이런 세로셈이 되는데요. 각 부분합이 자릿수가 겹치기 때문에, 일의 자리부터 적고, 십의 자리는 기억해 두었다가 2단계 계산 끝나면 합해서 십의 자리를 채워주고, 백의 자리는 또 기억해 두었다가 3단계 계산이 끝나면 최종 답을 달아주는 방식으로 진행됩니다.

십의 자리가 같은 두자리 숫자들의 곱을 알아봤습니다. 이 중에서 단연 쓰기 편한 것은 십의 자리는 같고 일의 자리 합해서 10이 되는 경우의 암산법이겠죠. 특히 끝자리 5인 (그래서 합하면 10이 되는) 두자릿수의 제곱을 아주 편하게 계산할 수 있습니다.
15 x 15 = 225
25 x 25 = 625
35 x 35 = 1225
...
95 x 95 = 9025
손으로 직접 써 봐야 익숙해지니, 아무 숫자나 잡아서 한 번 해 봅시다. 끝.
