초등학교 때 방학이면 항상 탐구생활이라는 방학용 교재에 대한 방송이 EBS에서 나왔었습니다. 거기에서 운만 띄우고 갔던 수학 트릭 문제 하나 여기 나갑니다.
마법사가 와서 말했습니다.
일의 자리와 백의 자리 차이가 1이 넘는 세자리수 아무거나 생각해봐.
[step 1] 그리고 그 숫자를 뒤집어서 (예를 들어 처음 생각한 수가 123이면 321로) 처음 숫자와의 차이를 구해.
[step 2] 그렇게 나온 차이값을 다시 뒤집어서 더해.
자.. 이제 네 마음을 들여다 보니, 그 답은 1089!
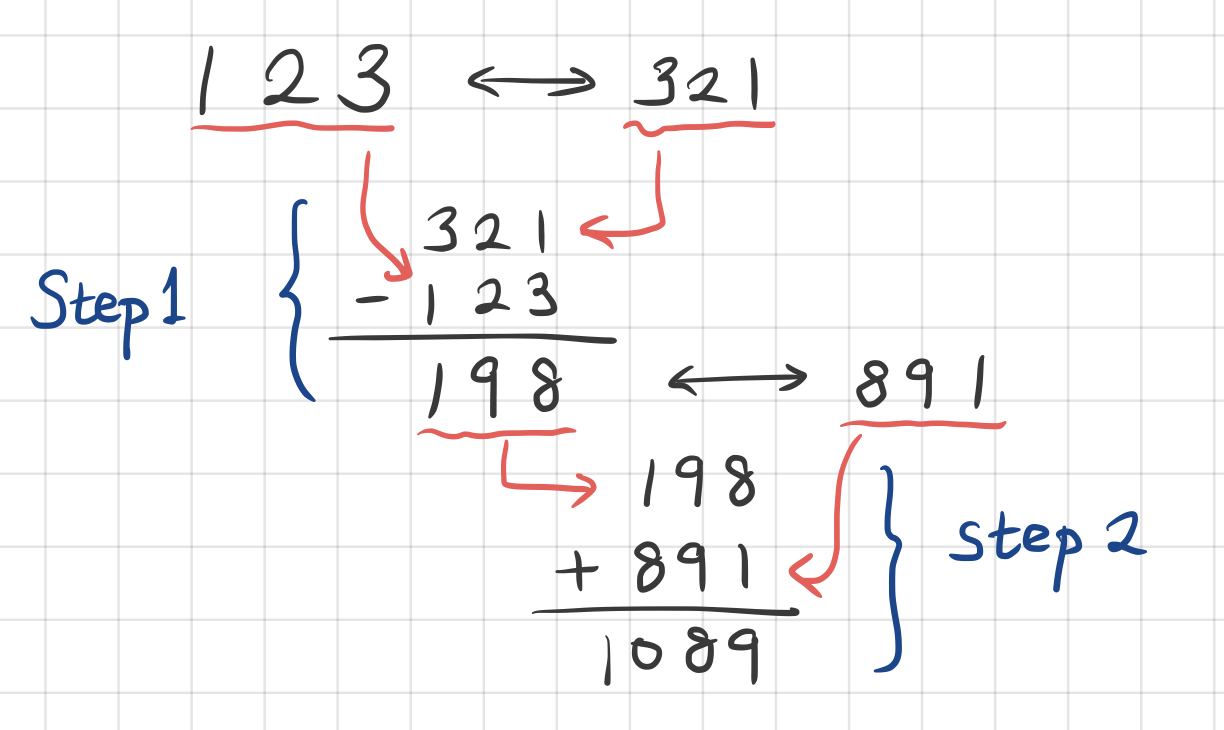
이 트릭의 놀라운 점은 중간 계산 결과를 물어보지 않는다는 겁니다. 보통 수학 트릭들은 "이렇게 계산해봐 저렇게 계산해봐"라고 한 다음에 결과를 물어보고 대답을 듣자 마자 처음에 생각한 숫자를 맞추는 형식인데요. 이 트릭에는 그런 것이 없죠. 마치 독심술을 한 것 처럼요.
초등학교(아재용어로 국민학교) 때 방학이면 늘 탐구생활이라는 방학용 교재를 설명하는 늘 똑같은 방송이 있었는데요. 거기에서 이 트릭을 저렇게 운만 띄우고 가 버렸었습니다. 몇 번 숫자를 다르게 넣어서 해 보면, 독심술이 아니라 항상 답이 1089가 된다는 걸 알 수 있지만, 무려 EBS에서 왜 그렇게 되는 지는 안 가르쳐 주고 그냥 넘어가 버리다니요. 좀 야속했더랬죠.
그래서 어린 마음에 이유를 알지못하는 트릭에 대한 마음의 짐을 지고, 이것도 언젠가 알 수 있겠지하고 버킷리스트에 넣어 놓았었는데, 이 트릭의 증명은 좀 까다로워서 문자로 된 식을 배운 이후에도 한참이나 (1년 정도) 증명을 못하다 갑자기 떠오른 단서가 있어서 겨우 겨우 방법을 찾아냈었던 기억이 납니다. 대수적인 증명은 1089 Magic Trick에서 했지만, 저희 아이도 좀 버거워하더군요. 중간에 이런 살짝 긴 문자로 된 식이 나와서요.
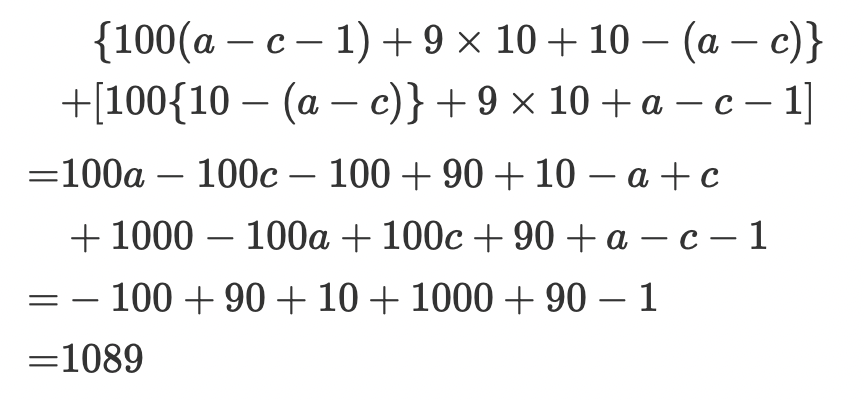
그래서 이번 글에서 좀 더 짧게 쉬운 버전을 만들어봤습니다. 영미권에서는 1089 Magic Trick이라는 이름으로 불리는 이 트릭, 그럼 증명을 시작해볼까요?
처음에 생각한 숫자를 abc라고 합시다. 그리고 이것을 뒤집은 숫자는 cba가 되겠죠. 증명을 간단하게 하기 위해서 abc > cba 인 경우(abc가 cba보다 큰 경우)만 생각하겠습니다. Step 1에서 처음 숫자와 뒤집은 숫자의 차이를 구한다고 했기 때문에 예를 들어 321을 처음 생각해서 123과의 차이를 구하는 것이나, 123을 처음에 생각해서 321과의 차이를 구하는 거나 뒷과정이 똑같겠죠. 이렇게 증명을 훼손하지 않으면서 범위를 줄이는 것을 "일반성을 훼손하지 않고" 줄였다고 이야기하고요. 영어로는 Without loss of generality라고 말하고, 하도 자주 쓰여서 WLOG라고 줄여쓰기도 합니다.
이제 step 1에서 말하는 대로 abc에서 cba를 뺄 건데요. cba를 한꺼번에 빼지 말고, cb0를 빼고 a를 나중에 빼는 것이 포인트입니다. 예를 들어 처음 생각한 숫자가 321이었다면 뒤집은 숫자는 123인데, 이것의 차이를 구할 때, 321-123을 한 번에 하는 것이 아니라 321-120을 먼저 하고 그 결과에다가 3을 마저 빼 주는 겁니다.
먼저 abc-cb0를 하면 이렇게 됩니다.

여기에 a를 마저 빼려고 하는데, 문제가 하나 있죠. abc > cba인 경우를 생각하고 있으니 a가 c보다 큽니다. 그래서 끝자리가 c인 숫자에서 a를 바로 뺄 수가 없죠. 초등학교 산수시간을 떠올려보면, 이럴 때 어떻게 하던가요? 앞자리에서 빌려옵니다. 그런데 앞자리가 0이네요. 그러면 그 앞자리에서 다시 빌려오고, 아까 0이던 자리는 9가 되죠. 이렇게요.
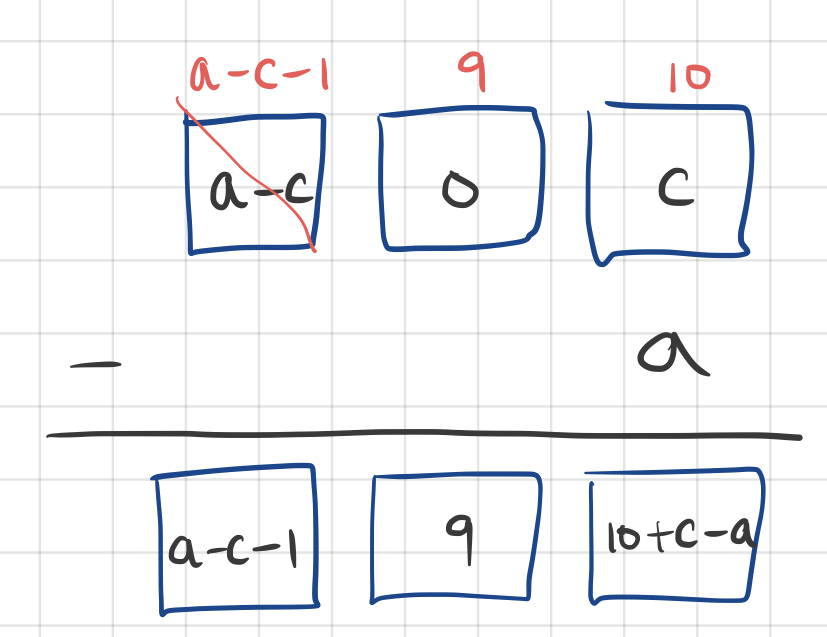
그래서 두 수의 차이를 구했습니다. 이제 이 결과를 뒤집어서 더하면 되겠죠.
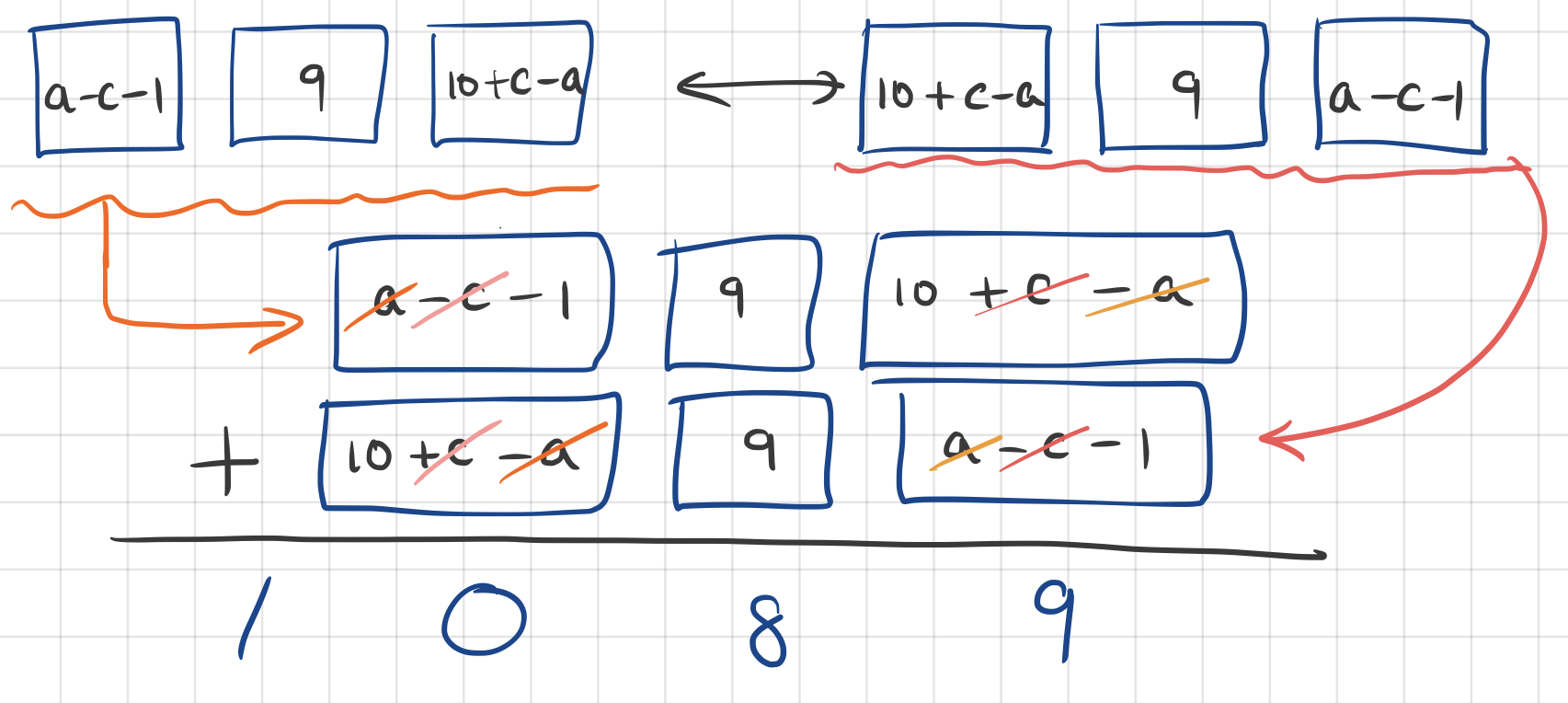
더하면 마술처럼 같은 문자들이 다 상쇄되고 답이 1089가 됩니다. 문자를 도입했는데 최종결과에 아무 문자도 안들어있다는 것은, 그 문자와 상관없이 답이 그렇게 나온다는 뜻이죠. 그래서 abc가 무엇이든지에 상관없이 (물론 몇 가지 조건은 있지만요) 답은 1089가 됩니다.
매직트릭에서 처음 숫자를 생각할 때 백의 자리와 일의 자리 차이가 1이 넘어야 한다는 조건이 있었지요. step 1이 끝나고 두 수의 차이를 구했을 때 백의 자리가 (a-c-1)의 형태로 나와서 그렇습니다. 차이가 딱 1이 되면 저 부분이 0이 되어서 세자리수가 안 만들어지고요. (예를 들어 231-132 = 99) 백의자리와 일의 자리 차이가 0이 되면, 숫자를 뒤집어도 같은 숫자가 나오기 때문에 차이가 0이 되어버려서(예를 들어 121 - 121 = 0) 트릭이 깨집니다. 그래서 백의 자리와 일의 자리 차이가 1이 넘어야 한다는 조건이 붙게 됩니다. 끝.
이 트릭은 증명이 더 트릭입니다. 무턱대고 처음 숫자 abc를 100a + 10b + c 로 놓고 시작하면 step 1 끝나자마자 99a - 99c가 나와서 그 다음 진행을 어떻게 해야 할 지 감이 안 잡히죠. 1089는 트릭 그 자체만으로도 재미있으니 한 번씩 써 봅시다. 진짜 끝.
