숫자를 수직선에 다 찍으면 직선이 되는 줄 알았더니...
이야기를 시작하기 전에 그래프를 어떻게 그리는 지 되짚어 봅시다.
그래프란 사실 간단한 거에요. 숫자 하나마다 점 하나를 찍어 놓은 것이죠.
숫자 하나에 점 하나
숫자 1이 있다면,

숫자 2가 있다면,
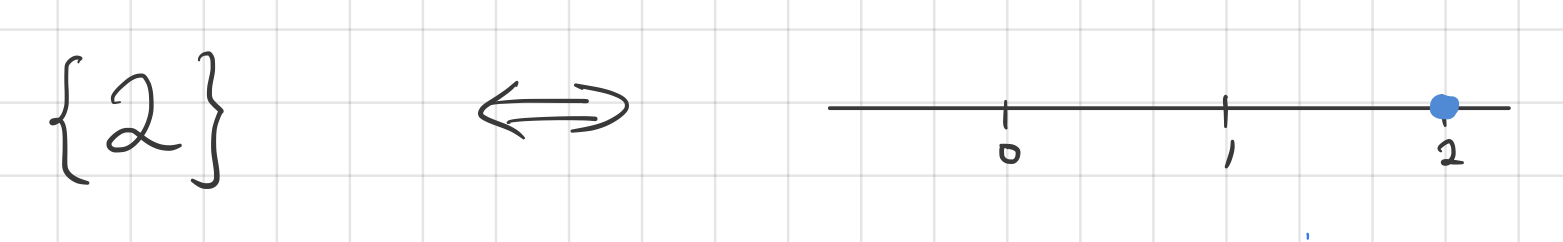
숫자가 여러개 있다면, 점도 여러개 나옵니다.
숫자 1, 2가 있다면
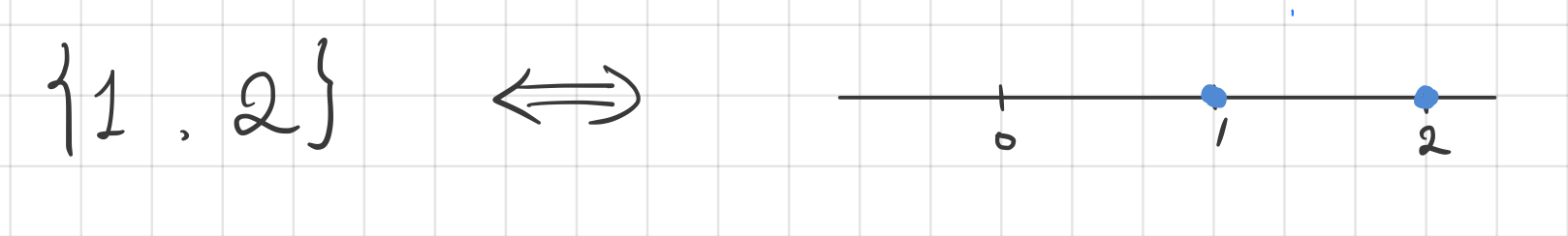
이 즈음에서 숫자 여러개를 표현하는 방식을 고민하게 됩니다. 만약 숫자가 1000개쯤 있으면 어떻게 해야 할까요? 1000개를 다 쓰기에는 시간이 너무 오래 걸리니, 혹시 그 1000개의 숫자들이 어떤 규칙이나 패턴이 있지 않은지를 살핍니다. 만약 그 1000개의 숫자가

이렇게 많은 숫자라도 규칙이 있다면 짧게 표현할 수 있습니다(1000개 다 써도 되지만요). 그럼 이걸 그래프로 그리면 어떻게 될까요? 저는 손으로 그리지는 않으렵니다. 이런 건 컴퓨터를 시켜야...

직접 찍든, 컴퓨터로 그리든, 점 1000개를 다 찍어야 해요. 엄청나게 찍어놓으니 언뜻 보면 하나의 선으로 보이네요.
그렇다면 점이 무한히 많은 경우는 어떻게 할까요? 예를 들어 "0이상 5이하의 유리수"라고 해 봅시다. 0과 5 사이에는 무한히 많은 유리수가 있습니다. 간단히 생각해 보면, 0이랑 5 사이의 무슨 숫자 두 개를 생각하든 항상 그 사이에 들어갈 숫자를 찾아낼 수 있잖아요. 이걸 무한 반복할 수 있으니 갯수가 무한하다는 것은 쉽게 알 수 있습니다. 갯수가 무한하니 이걸 하나씩 나열해서 수를 표현할 수는 없을 겁니다. 이런 경우에는 반드시 규칙을 찾아서 표현해주어야겠지요. 이렇게요.
{x | x는 0이상 5이하의 유리수}
숫자 집합의 표현은 이렇게 하면 짧게 써 지는데, 이걸 그래프로는 어떻게 그릴 수 있을까요? 아까 숫자 1000개일 경우에도 다른 방법이 마땅치 않아서 1000개 점 다 찍었는데, 정말 점을 무한번 찍고 있어야 할까요?
아마도 어디선가 점이 무한번 모이면 선이 된다는 것을 들어보았을 겁니다. 꽤 직관적이기도 하고요. 그래서 이 무한개의 숫자를 그래프로 표현하는 것은 오히려 쉬워보입니다. 0이란 지점에서 5라는 지점까지 직선으로 쭉 이어 그으면 표현이 되는 것 같으니까요.

그런데 말입니다. 그렇게 하면 안 됩니다.
아까
숫자 하나에 점 하나
로 표현한 것이 그래프라고 했습니다. 이것은 반대로도 적용이 되는데요. 그래프를 그렸다면 그 그래프의
점 하나에 대응되는 숫자 하나
를 반드시 찾을 수 있어야 합니다.
피타고라스 시절까지만 해도 정수의 비, 즉, 유리수만으로 행복했습니다. 그런데 피타고라스의 큰 업적인 피타고라스의 정리가 오히려 이 행복한 유리수 세상을 깨부수게 되죠.
아까 그어 놓은 선분 위에 가로세로 길이 1인 정사각형을 올려 놓습니다.

이 정사각형의 대각선의 길이를 x라고 하면 피타고라스의 정리에 의해서
이 되어야 합니다. 등호 왼쪽을 정리하면
가 되므로 대각선의 길이 x는 제곱하면 2가 되는 그 어떤 숫자가 됩니다.
이제 이 정사각형을 왼쪽 하단 꼭지점을 중심으로 회전시켜서 대각선이 정확하게 아까 그어놓은 선분에 일치하게 만들어줍니다. 그러면 그림에서 볼 수 있는 것 처럼 대각선의 길이가 0과 5를 잇는 선분 중간 어디 즈음에 위치한 한 지점이라는 것을 알 수 있습니다.

그 숫자가 대충 얼마 정도 되는 지도 알 수 있습니다. 제곱해서 2가 되는 어떤 숫자이니, 제곱해서 1이 되는 1보다는 클 것이고요, 제곱해서 4가 되는 2보다는 작을 겁니다. 1.xxx 의 형태가 될 거라는 이야기죠. 그런데 이런 숫자가 유리수 세상에 있을까요?
제곱하면 2가 되는 수가 유리수라면 정수의 비, 즉 분자와 분모가 정수인 분수로 표현할 수 있습니다. 여기서는 대각선의 길이를 생각하고 있으므로 음수를 생각할 필요가 없으니, 분자도 자연수, 분모도 자연수인 분수로 표현이 될 거라는 이야기죠. (둘 다 음수가 되는 경우는 둘 다 양수인 경우로 변환이 되기 때문에 따로 생각하지 않아도 됩니다)
이 숫자를 x로 두고 이 숫자의 분수 표현형태에서, 분자를 a 분모를 b라고 해 봅시다.
x를 제곱하면
그런데 이 값이 2가 된다고 했습니다. (제곱하면 2가 되는 수를 제곱했으니까요)
양변에
이제 여기서 이게 말이 안 된다는 것을 알게 됩니다.
자 생각해 봅시다. a, b가 자연수라고 했으니 소인수 분해(prime factorization)를 할 수 있습니다. (예를 들어 12라면
그럼 어디서 잘못된 걸까요? 쭉 맞는 방법으로 풀었는데, 그냥 가정만 하고 넘어온 부분이 한 군데 있었습니다.
제곱하면 2가 되는 수가 유리수라면
다른 게 다 맞으니 틀린 곳은 유리수라고 가정한 이 부분밖에 없는 것이죠. 그래서 제곱해서 2가 되는 수, 즉, 우리가 이미 배워서 아는
이 말은 무슨 말이냐 하면, 우리가 아는 수의 세상을 유리수 세상으로 한정하게 되면 그래프에서 선을 그으면 안 된다는 뜻입니다.
둘 중 하나를 선택해야 하죠. 유리수말고 수가 더 있는 것 같으니 그것까지 다 포함해서 수라고 하던가, 그래프 그릴 때에는 점만 무한히 찍고 앉아 있던가: 다른말로 그래프를 포기하던가.
유리수가 아닌 수의 발견이 피타고라스 정리에서 출발한 것이니 당연히 피타고라스학파에서도 이 내용을 알고 있었습니다. 하지만 그 동안 정수의 비로 세상의 모든 것을 설명하려던 (세상 만사 물이라고 한 탈레스보다는 이들이 백배 낫다 싶습니다만) 열망을 버리지 못하고 이 사실을 쉬쉬하게 되죠. 그래서 그림은 그림대로 그리고, 수는 여전히 유리수로 한정합니다. "측정가능한 길이에 대응되는 유리수가 없는 경우도 있다"라는 것은 피타고라스 학파 안에서는 공공연한 비밀이 되는데, 이걸 세상에 알리려고 했던 히파수스는 동료들에 죽임을 당합니다. 무섭죠.
중등교과에서는 이 부분을 좀 어물쩡하게 넘어갑니다. 분명히 유리수까지밖에 안 배웠는데, 부등식을 수직선 위에서 반직선을 그어가면서 익히고, 1차식과 그래프도 직선을 그어가면서 배우고 있죠. 그런데 또 대놓고 거짓말을 하는 건 아니더군요. 그래프를 그리는 어느 예제를 보아도 그냥, x와 y를 언급할 뿐 그게 유리수인지 실수인지 명시하지 않습니다. 하지만 분명한 것은 숫자를 실수범위로 가정해야 직선이든 곡선이든 선을 그을 수 있다는 겁니다.
너무 깐깐한 것이 아닌가 싶기도 하지만, 정작 우리가 부등식에서

물론 이렇게 넘어가는 이유가 있습니다. 유리수만으로 선을 표현하기엔 여기저기에 빈 틈이 있다는 것은 쉽게 밝힐 수 있지만, 무리수가 그 빈틈을 모두 메워준다는 것은 또 다른 차원의 이야기이기 때문입니다.
하지만 어물쩡하게 넘어간 탓에
을 간략하게 나타낸 것, 즉
숫자와 그래프 상의 점은 1:1 대응입니다. 무한개의 숫자를 다 쓸 수가 없어서 그 숫자의 규칙을 적어 놓는 방법 중의 하나가 식 혹은 관계식이고, 그래서 식을 만족하는 각 점과 그래프의 상의 점이 또한 1:1 대응입니다. 관계식 뿐만 아니라 방정식도 그래프로 이해할 수 있고, 반대로 도형을 식으로 이해할 수도 있습니다. 같이 배우면 한 사실에 대한 두가지 관점이라서 한쪽의 지식이 다른쪽의 지식을 강화해주죠. 그런 의미에서 둘째에게 벡터를 살짝 가르쳐주고 있습니다. 어차피 도형이라 쉽기도 하고요. 벡터를 좋은 시점에 알기 시작하면 도형의 길이와 면적, 그리고 좌표계를 한 덩어리로 이해할 수 있게 됩니다. 이 부분은 다음 기회에 정리해 보도록 하지요.
아무튼, 요약하면,
유리수만 머릿속에 있다면, 그래프 그릴 때 선을 그으면 안 됩니다. 자연수만 생각할 때 선을 긋지 않고 점만 찍는 것과 같은 원리입니다.
선을 그었다면 그 안에 유리수도 있고, 무리수도 있습니다.
숫자와 그래프 상의 점은 1:1대응입니다.
끝.
