요즘 아이들은 π가 무리수인 것도 알고, π소수점을 외우고 다니는 사람들도 있습니다. 3.14159265358979... 그런데 π가 3.14즈음되는지 직접 해 본 사람은 몇이나 될까요? 그냥 외우기만 한 게 아닐까요?
원의 지름에 대한 원 둘레 길이의 비를 원주율이라고 하고 옛날부터 사람들이 그 비율이 3이 조금 넘는다는 것을 알고 있었습니다. 요즘은 학교에서 그 비율이 3.14정도 되고, 정확하게 표현하려면 소숫점이 끝도 없고 반복도 없어서, 즉 무리수라서, 직접 소숫점을 다 쓰지 않고 π라는 기호로 쓴다는 것도 가르쳐 줍니다. 그런데 정말로 이 값이 3.14즈음되는지 알아본 사람은 얼마나 될까요?
이번 글에서는 원주율, 우리가 π로 부르는 그 값이 정말 3.14 언저리가 되는지 알아보겠습니다.
기본 원리는 간단합니다. 원의 둘레길이와 지름을 잘 재어서 둘레길이를 지름으로 나누어주면 원주율이 되니 실제로 그렇게 하기만 하면 될 겁니다.
일단 우리가 가지고 있는 도구들을 볼까요? 일단 집에 컴퍼스가 있는 경우를 생각해 봅시다.
평소에는 쓸 일이 많지 않지만, 많은 초등학생들은 집에 컴퍼스를 가지고 있을 겁니다. 일단 컴퍼스가 있으면 임의의 지름을 가지는 원을 그리기가 아주 쉽지요. 문제는 원 둘레길이인데요. 그려놓은 원 위에 실을 놓아서 한 바퀴 돌려준 후, 실을 자르거나 마커펜 등으로 실 위에 표시를 해 둔 다음 실을 쭉 펴서 자로 길이를 재면 되겠지요.
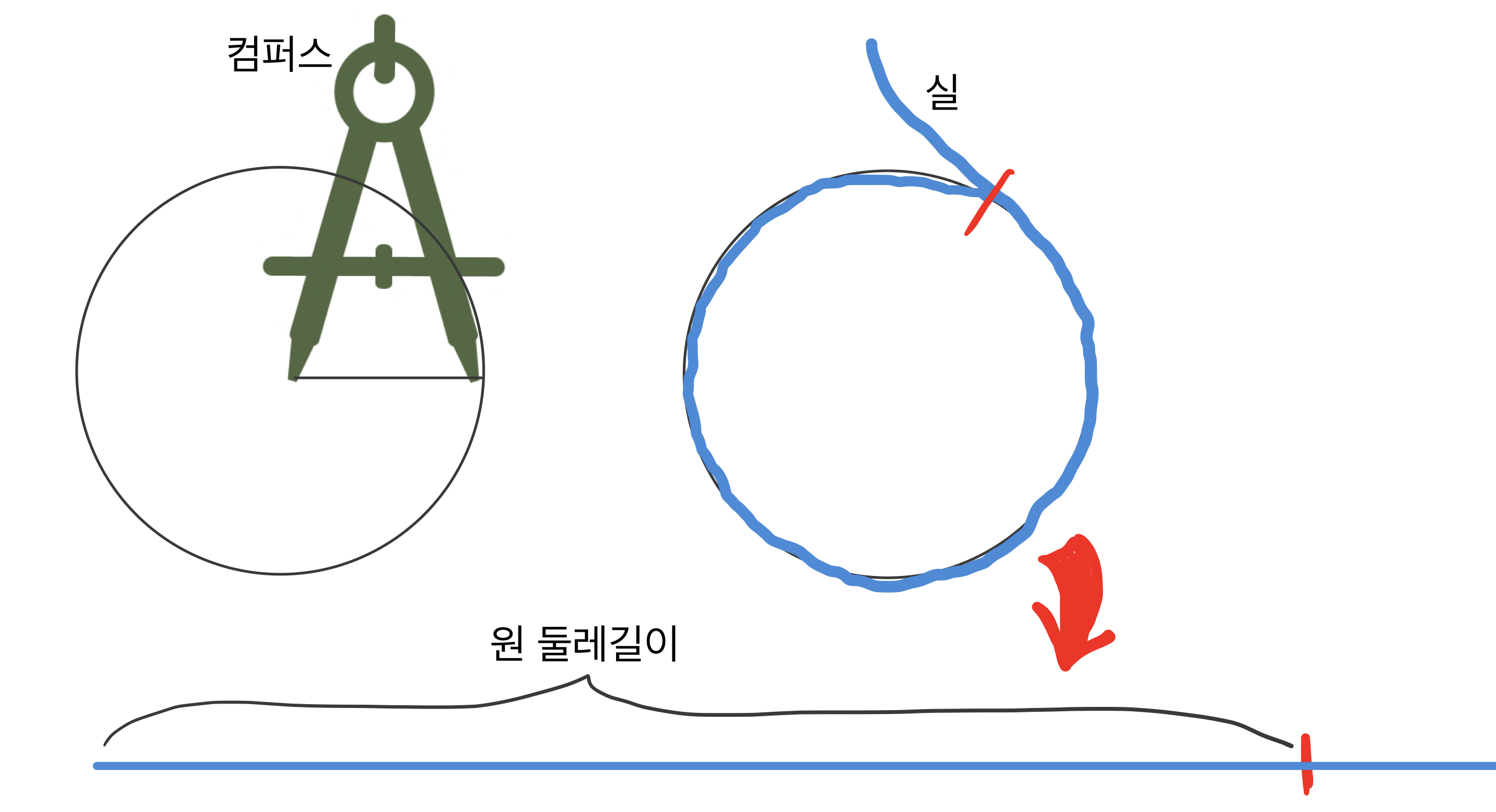
그런데 이게 잘 안 됩니다. 원 위에 딱 맞도록 실을 올려놓는 것도 어렵거니와, 보통 실을 원 위에 올려 놓을 때에는 약간 구불구불하게 놓게 되고, 당기지 않고 올려 놓으니 장력(tension)이 없는 상태로 올려 놓는데, 이것을 쭉 펴면, 구불구불했던 것이 펴져서 길이가 좀 더 길어지고, 장력이 작용해서 길이가 거기에서 좀 더 늘어나기 때문에, 원주율을 계산하면 실제 값보다 크게 나옵니다. 3.5 안 넘으면 다행이다 싶을 정도로요.
나무판 위에 컴퍼스로 원을 그리고 그려진 원 위에 작은 간격으로 얇은 못을 못 전체 길이의 반정도만 들어가도록 박아줍니다. 그리고 실을 못을 둘러싸도록 감싸서 길이를 잽니다. 줄자로 바로 재어도 되고요. 품이 많이 들지만 잘만 하면 3.5보다는 작은 비율을 구해낼 수 있습니다.
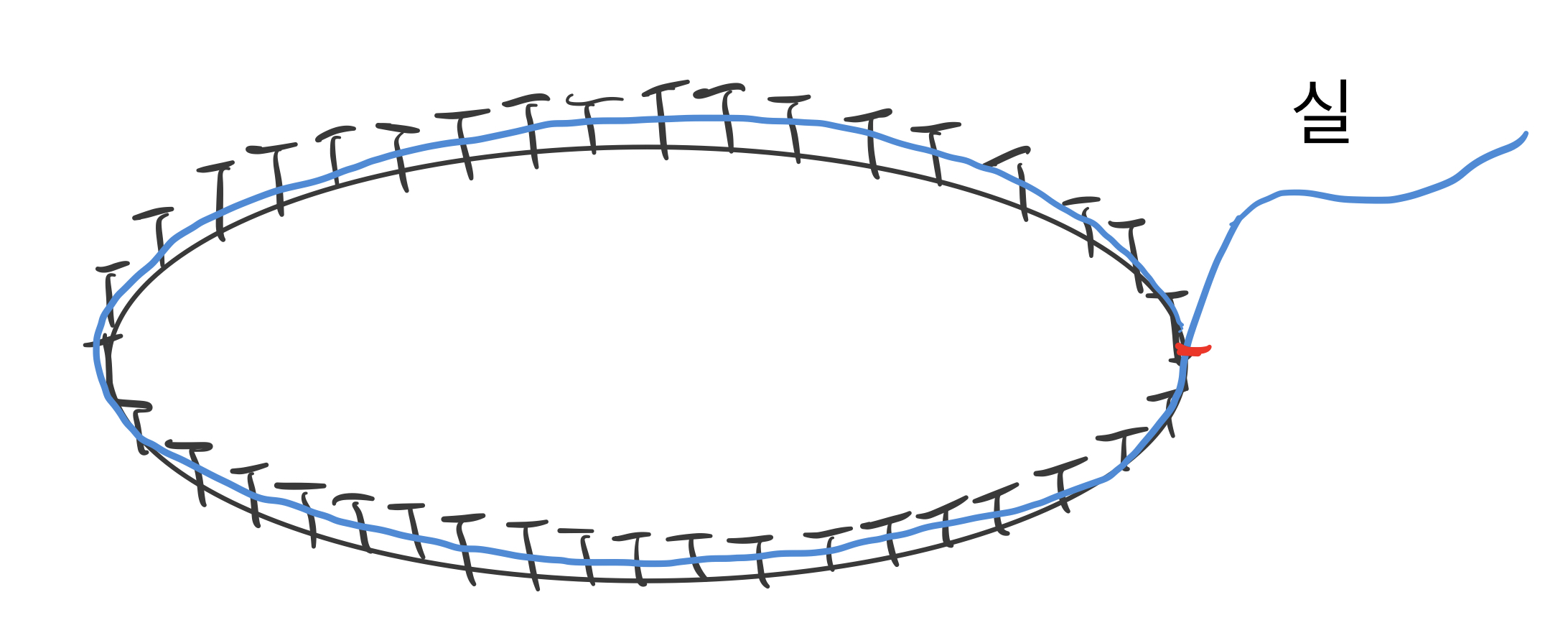
오차는 원 위에 못을 얼마나 촘촘하게 잘 정렬해서 박았는지, 그리고 못의 굵기에 따라 천차만별입니다. 못을 박을 때 의식적으로 못이 원 바깥으로 나가지 않도록 약간 안으로 박아주면 제법 정확하게 원 둘레 길이를 잴 수도 있지요. 하지만 앞에서도 말했듯이 준비물도 많이 필요하고, 품이 많이 듭니다. (게다가 원주율 계산해보면 3.14 안 나옵니다. 해 보세요)
그럼 집에 컴퍼스가 없는 경우 (이게 아주 일반적인 경우지요), 집안에 있는 동그란 물체를 가지고 원주율을 구할 수가 있습니다.

저는 컵을 예로 들어보겠습니다. 이제 둘레길이를 재는 것은 오히려 쉽습니다. 실을 팽팽하게 잡아 당기면서 둘레를 둘러주어서 길이를 잴 수 있겠죠. 컵이 원통형이 아니라면? (많은 경우 그렇죠) 실로 재면 미끄러져서 다른 둘레를 재고 있을 테니, 줄자가 있으면 제일 좋고요, 없으면 약간 빳빳한 리본 테입(저는 없으면 그냥 A4지를 길게 잘라서 만듭니다)으로 원 둘레를 두른 다음 재면 됩니다.
가장 문제가 되는 것은 지름을 재는 것이지요. 원을 컴퍼스로 직접 그린 것과는 다르게 이미 만들어진 도구는 원의 중심을 알기가 어렵거든요. 방금 예로 들었던 컵만 보더라도 안쪽은 비었으니 어떻게 원 중심을 지나가는 선의 길이를 잴 수 있을까요? 잘못 재면 지름이 아니라 현(chord)를 재게 될 테니까요.
두 가지 정도 쉬운 방법이 있습니다.
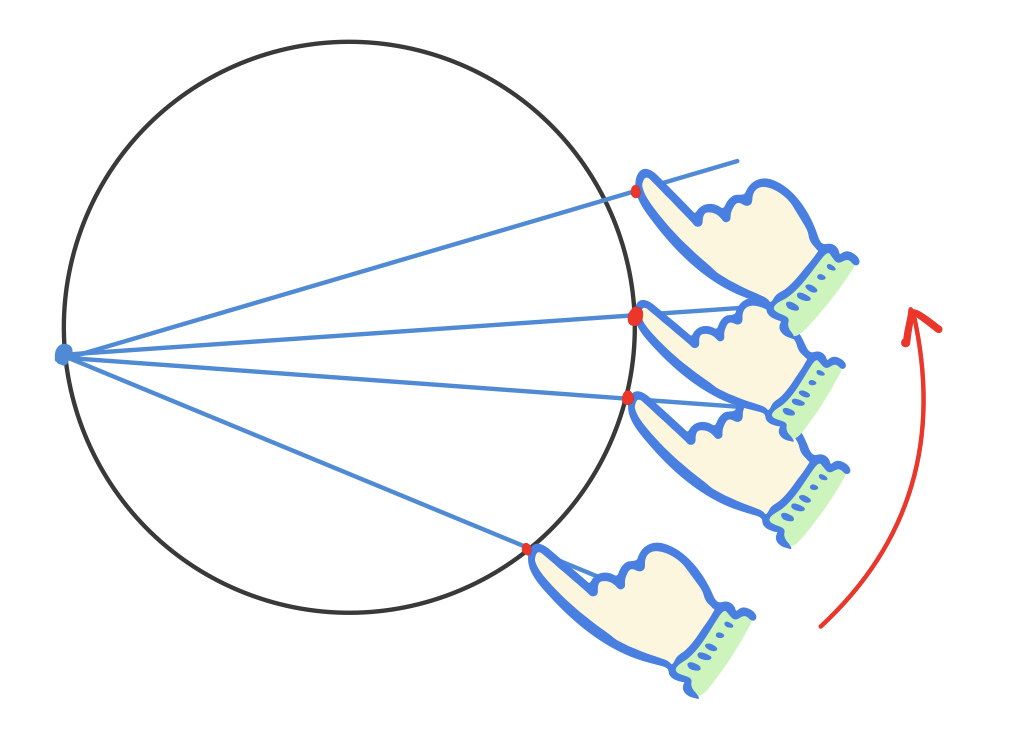
하나는 실로 지름을 재는 방법입니다. 실의 한쪽 끝을 원 위의 아무 지점에다가 고정합니다. 손가락으로 눌러도 되고 테입으로 붙여버려도 됩니다. 실의 다른쪽 끝을 조금 짧게 손톱으로 팽팽하게 잡아준다음, 원 둘레를 두르면서 실의 길이가 길어져야 돌아가면 잡은 부위를 좀 느슨하게 해서 길어지게 하고, 다만 더 짧아지지는 않게 합니다. 이거 말로 설명하기 어렵네요.
이것은 원 위의 두 점을 잇는 선분 중에서 지름이 가장 길다는 성질을 이용하는 겁니다. 제법 정확하게 지름의 길이를 잴 수 있습니다.
버니어(Vernier)가 생각나시는 분이 있을 지 모르겠는데요. 집에 있으면 사용하세요. 정확하게 지름 크기를 재어 줄 겁니다. 하지만 지금 이 글에서는 줄자도 있을지 없을 지 모르는 열악한 상황을 가정하고 있습니다.
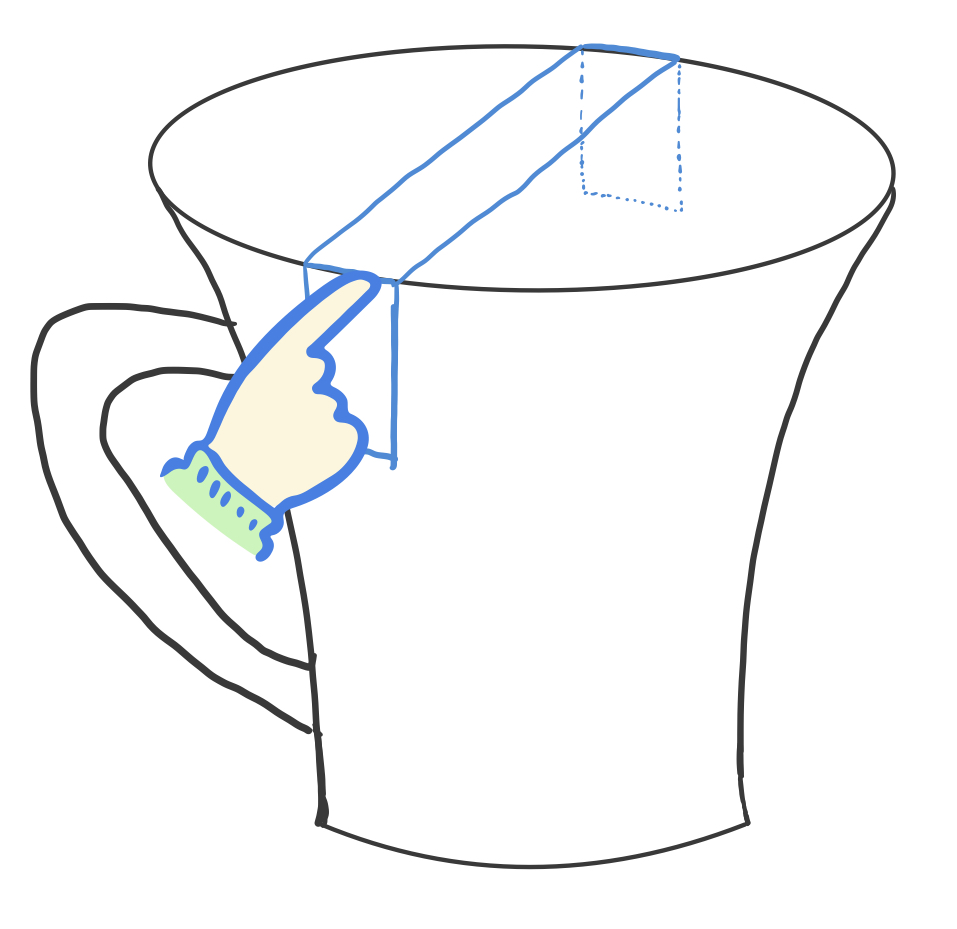
두 번째 방법은 종이리본을 이용하는 겁니다. 종이리본을 그림처럼 접어줍니다. 그리고 이걸 컵 위에 올려 놓은 다음 종이리본의 접힌 옆면을 지긋이 눌러줍니다. 그리고 그 상태에서 반대쪽을 원에 접하는 부분에서 접어 주고 그 사이 길이를 재면 됩니다.

이것은 왜 지름의 길이를 재어주느냐. 종이리본을 위의 그림처럼 접으면 접힌 부분과 종이리본이 나가는 방향이 수직이 됩니다. 원의 모퉁이 옆면을 종이리본의 접힌 부분과 함께 손가락으로 눌러주면 힘의 작용점과 같은 지점에 종이리본의 접힌 부분이 원 둘레와 접점을 이루게 됩니다. 원과 직선이 한 점에서 접한다면, 그 직선에 수직이면서 그 접점에서 시작한 직선이 원의 중심을 지나게 되어 있습니다.
둘째랑 같이 해 보았는데, 지름의 길이는 첫번째 방법으로 한 것과 두 번째 방법으로 한 것이 모두 8.5cm가 나왔습니다.
둘레길이는 종이리본으로 둘러서 재었는데, 처음에 둘째가 재었던 것은 좀 느슨했었거든요. 그래서 27.35cm가 나왔고, 제가 좀 더 당겨 재어서 26.95가 나왔습니다.
이제 원주율을 구해보면?
26.95 ÷ 8.5 ≈ 3.17
이거 3.14 안 나오죠?
집에 있는 원 모양으로 생긴 도구들 몇 가지로 해 보면, 3.14 구하는 게 절대로 쉬운 일이 아니라는 것을 알게 됩니다. (물론 도구의 모양이 완벽한 원이 아니라서 그럴 수도 있습니다. 하지만 보통은 측정 오류지요)
이 즈음에서 둘째가 물어보더군요.
이렇게 재도 안 되는데 도대체 그 옛날에는 이게 3.14 쯤 된다는 걸 어떻게 안 거에요?
아주 좋은 질문이네요. 이제 관념적인 방법을 사용할 때가 된 것 같습니다. 다음 글에서 아르키메데스 방법이란 걸 알아보겠습니다. 피타고라스 정리만 알면 다 할 수 있습니다.
시실 잘만 한다면 직접 측정해서 3.14의 비율을 구할 수도 있습니다. 우리가 가지고 있는 측정오차를 더 줄이는 데에는 한계가 있으니 원을 더 크게 그려서 상대적인 오차를 줄이면 되거든요. 하지만 컴퍼스로 그릴 수 있는 원의 크기나 집 안에 볼 수 잇는 동그란 도구들(프라이팬, 컵)은 충분히 크지 않기 때문에, 집 안에서 볼 수 있는 것들로 지름과 둘레길이를 재어서 원주율 3.14를 구하는 것은 보통 어려운 일이 아닙니다. 그래도 이렇게 해서라도 원주율이 3이랑 4 사이에 있는 숫자라는 것을 직접 경험하는 것이 중요합니다.
학창시절을 떠올려보면 지금 생각해도 참 운이 좋았던 것이, 만나는 선생님마다 아이들에게 직접 재어서 숫자를 눈으로 보게 하시더군요. (교육과정에 그러라고 되어 있었는지도 모르겠지만요) 초딩 때 원주율 처음 배울 때에는 직접 컴퍼스랑 실로 계속 재어서 원주율을 구해봤었고, 중딩때 제곱근을 배울 때에는 수업시간을 반 넘게 할애해서 제곱근 값을 직접 손으로 소숫점 셋째자리까지 구하게 시키는 선생님을 만났죠. 고딩이 되어서 싸인 코싸인 함수를 배울 때에도 눈금종이랑 자와 실을 들고 점을 수십개 찍고 직접 다 재어서 사인 그래프 그리는 숙제를 하던 기억이 나네요.
좀 지겨운 면도 있었지만 아직도 기억이 나는 걸 보면, 역시 관념적인 것을 어떻게든 시각화하고 경험으로 만들어내는 건 그 값어치를 하는 것 같습니다. 끝.
