지난 시간에는 일상생활에서 볼 수 있는 원을 열심히 재어서 원주율을 계산해 봤습니다. 하지만 소숫점 둘째자리까지 맞아들어가는 결과를 얻지는 못했죠. 측정 오류이거나 정확하게 원이 아닌 걸 재어서 그런 것인데요. 오늘은 수학적으로 접근해서 3.14에 근접한 답을 내 보겠습니다. 몇 번 만에 된답니다.
아래 그림을 보시죠
원의 둘레 길이를 계산할 때 자주 볼 수 있는 그림입니다. 직관적으로 원에 내접한 정다각형(빨간색으로 표시)의 둘레 길이보다는 원 둘레 길이가 더 길 것이고, 원에 외접한 정다각형(파란색으로 표시)의 둘레길이보다는 원 둘레 길이가 작을 것이라는 것을 직관적으로 알 수 있습니다. 이것을 이용해서 원 둘레 길이의 범위를 알 수 있지요.
그리고 정다각형의 모서리 갯수가 많아질 수록 정다각형의 둘레 길이는 원 둘레 길이에 근접하기 때문에, 모서리 갯수가 증가하면 범위가 좁아지면서 원 둘레길이를 점점 더 정확하게 알아낼 수 있게 됩니다.
그런데 보통 거기까지 생각한 후에 더 이상 진행을 하지 않죠. 정삼각형, 정사각형, 혹은 정육각형까지는 어느정도 쉽게 머릿속에 들어오지만, 그보다 많은 꼭지점을 가진 다각형에 대해서는 삼각함수를 자유롭게 사용하지 않는 이상, 둘레 길이를 어떻게 구하는지 감을 잡기 힘들기 때문이죠.
오늘은 삼각함수를 사용하지 않고 피타고라스정리만 이용해서 원주율이 3.14에 근접하게 된다는 걸 알아보겠습니다.
쉬워 보이는 이 문제는 무려 옛날 동경대 입학 시험문제 중에 하나였답니다.
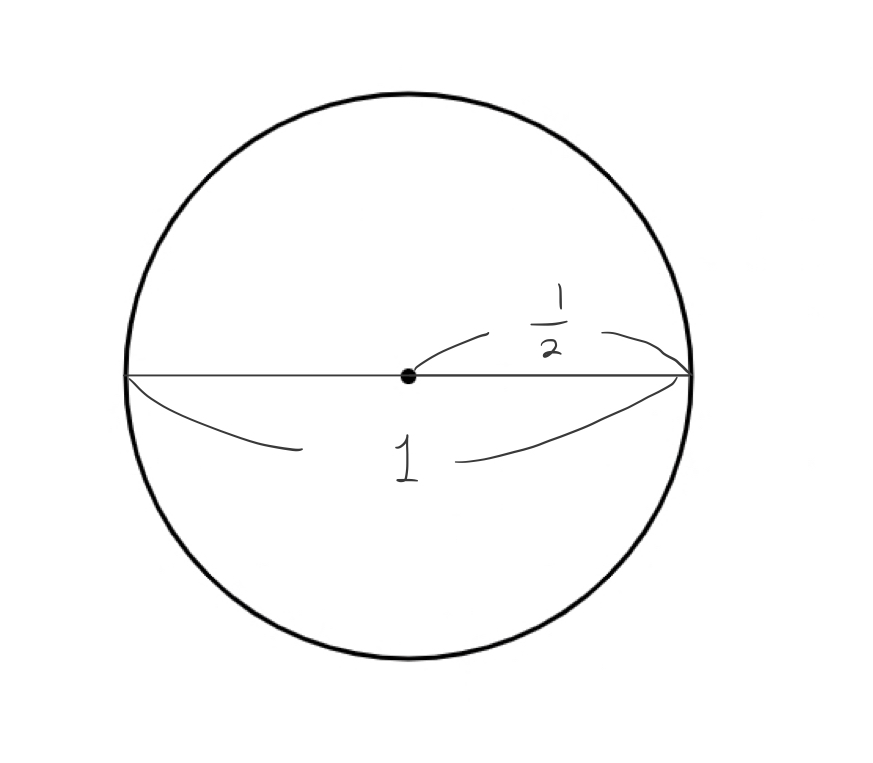
우선 반지름이 1/2인 원을 하나 그립니다. 반지름 1/2으로 하는 이유는 지름이 1이 되어서 원의 둘레 길이를 구한 것이 원주율을 구한 것과 같아지기 때문입니다.
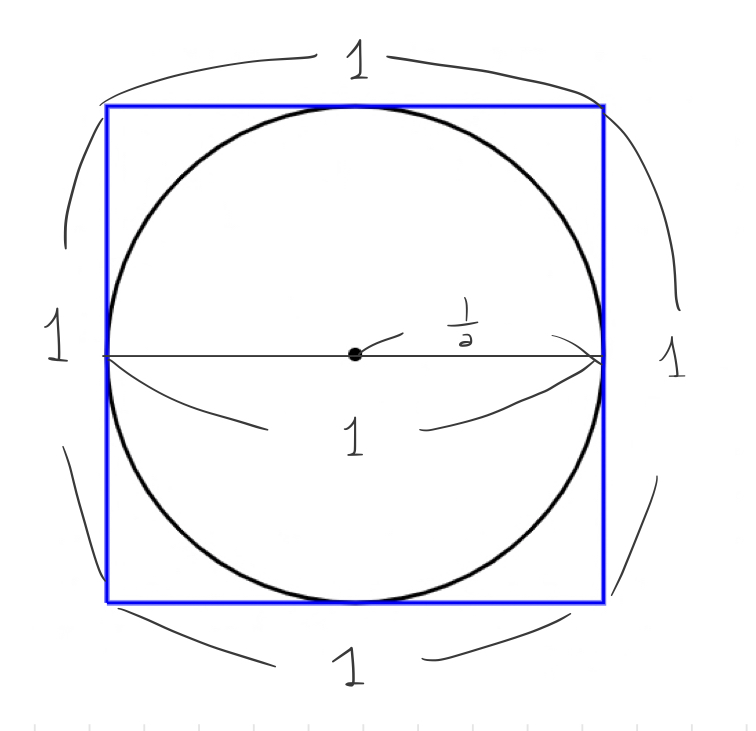
먼저 4보다 작다는 걸 보여볼게요. 위 그림 처럼 원의 외접다각형으로 정사각형을 그려줍니다. 원의 지름이 1이기 때문에, 정사각형 한 변의 길이가 1, 즉, 둘레길이가 4가 됩니다. 원둘레 길이(여기서는 원주율)이 4보다 작다는 게 쉽게 보여졌습니다.
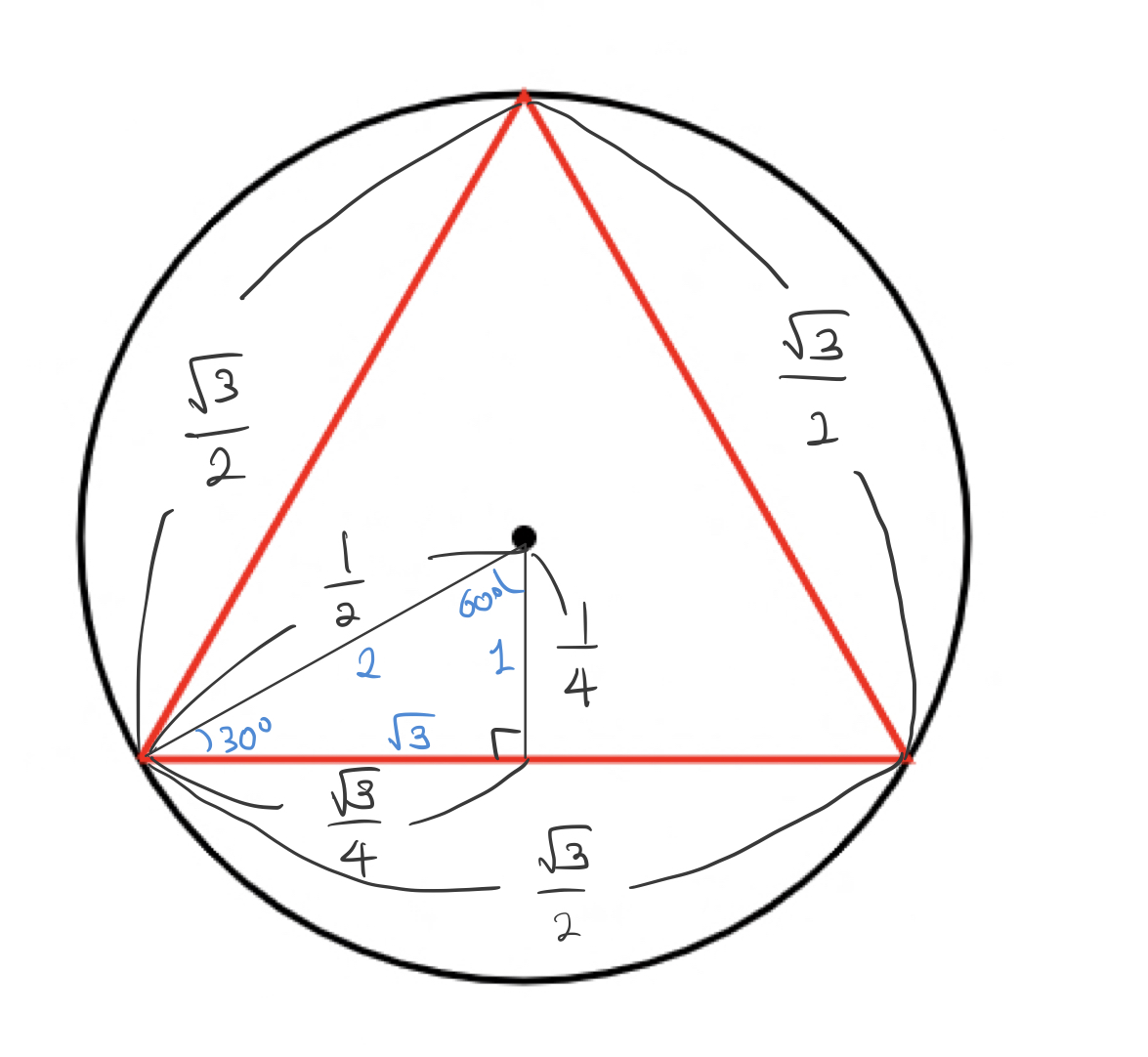
자, 그럼 원 안쪽에는 어떤 도형을 넣어야 3보다 크다는 걸 알 수 있을까요? 윗 그림처럼 삼각형을 넣어볼까요? 이 원에 내접하는 삼각형의 둘레길이는 30도 60도를 가지는 특수 직각삼각형의 길이의 비(1 : 2:
정사각형을 넣어보면? 안 됩니다. 정오각형을 넣어보면? 정 오각형은 삼각함수를 모른 상태에서는 둘레 길이구하기가 여간 어려운 게 아닙니다. 오히려 정육각형이 쉬워요.

정육각형을 넣으면, 정육각형은 도형 중심에서 꼭지점까지 선을 그어보면, 정삼각형 6개가 모인 모양이지요(증명생략). 그래서 각 변의 길이도 1/2이 됩니다. 1/2이 6개 있으니까 딱, 3이 되죠.
그래서 원에 내접하는 정육각형을 그리고, 원에 외접하는 정사각형을 그려서 각 둘레 길이를 구하면, 원주율이 3보다 크고 4보다 작음을 알 수 있습니다.
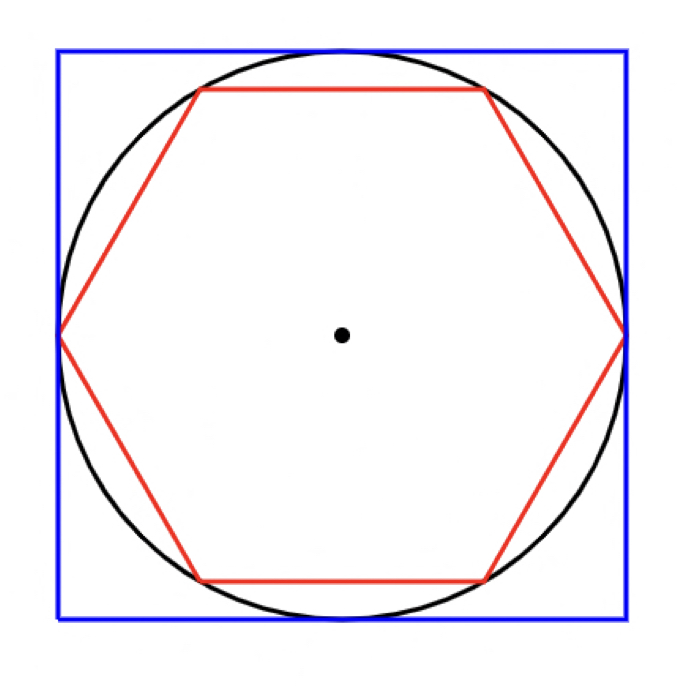
정육각형모다 더 많은 꼭지점을 가지는 다각형 중에서 둘레길이를 쉽게 구할 수 있는 게 뭐가 있을까요? 사실 여기까지 생각하고 나면 조금 좌절스럽기까지 합니다. 정육각형씩이나 구했는데, 3.1xx도 아니고 3에서 멈춰버리니, 도대체 몇각형까지 가야 3.14에 근접하는 걸까요?
이 즈음에서 아르키메데스가 옛날에 쓰던 방식을 끌고와 보겠습니다.
편의상 설명할 때에는 내접 정삼각형에서 시작하겠습니다.
우리가 뭘 할 것이냐 하면요. 정삼각형의 둘레 길이를 알고 있다고 할 때, 꼭지점 갯수가 두 배가 되는 정육각형의 둘레 길이를 바로 구해버릴 겁니다.
정삼각형의 꼭지점 3개는 그대로 유지하고요, 나머지 3 개의 꼭지점은 각 변에서 수직 이등분선을 그어서 원과 만나는 지점을 꼭지점으로 추가하는 것이죠. 이렇게 하면 내접 정육각형을 쉽게 만들 수 있습니다.

그렇다면 새로운 정다각형의 한 변 길이는 어떻게 구할까요?
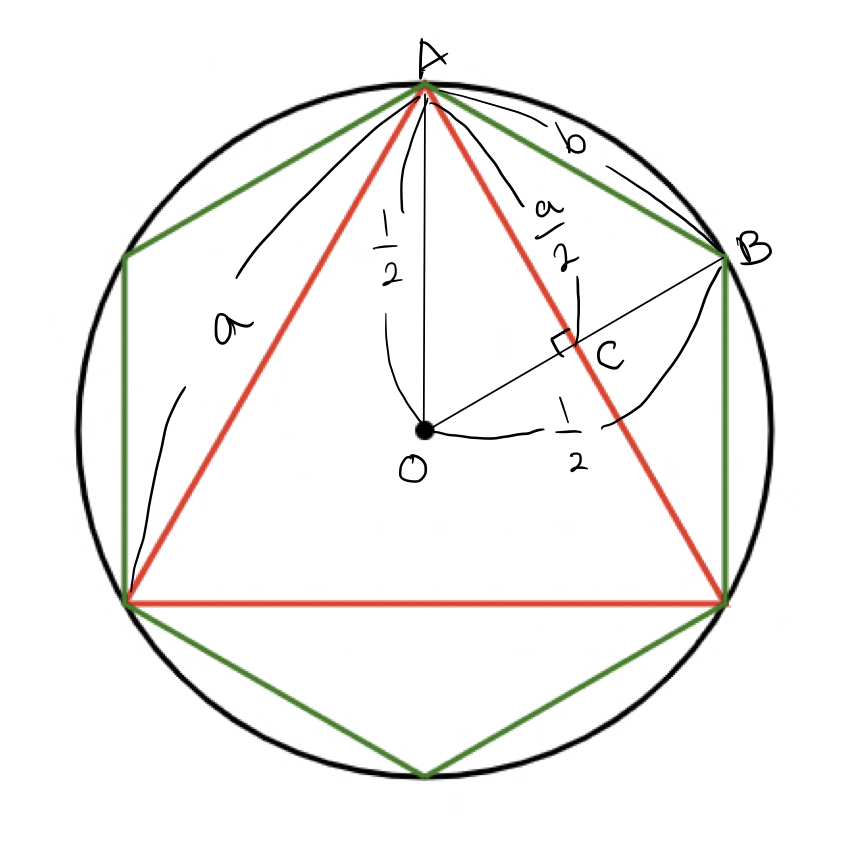
우리는 여기서 빨간색으로 표시한 길이를 아는 상태에서 시작해서 새로운 정다각형의 한 변의 길이 b를 구할 겁니다.
원의 반지름은 1/2로 잡고 시작할 것이고요. 원래 정다각형(이 예제에서는 정삼각형)의 한 변의 길이를 a라고 합시다. 그럼 변 AO는 반지름과 같아서 1/2이고 변 AC는 한 변 길이의 절반이라서 a/2가 됩니다. 삼각형 AOC가 직각삼각형이니 피타고라스정리에 의해서
변 BO의 길이는 반지름과 같은 1/2이고 변 OC를 빼면 변 BC의 길이가
변 BC의 길이를 알았으니 직각삼각형 ACB에서 피타고라스 정리를 이용하면 새로운 정다각형의 한 변의 길이를 알 수 있게 됩니다.
좋은 점은 이것이 정삼각형에서 정육각형으로 갈 때이든 정육각형에서 정 12각형으로 갈 때이든 식이 동일하다는 겁니다. 그래서 같은 식을 반복해서 꼭지점이 많은 다각형의 한변 길이, 그리고 그것을 통해 아주쉽게 그 둘레 길이를 구할 수 있다는 것이죠.
그리고 한 번 식을 적용할 때마다 꼭지점수가 2배 증가하거든요. 그래서 3각형 6각형 12각형 24각형, 48각형, 96각형 순으로 매우 빠르게 원의 둘레 길이에 근접할 수 있습니다.
식은 복잡해 보이지만 여기서 사용되는 복잡한 연산자는 제곱근 밖에 없구요. 제곱근은 옛날부터 표로 정리되어 있었습니다. 사실 표가 없어도 시간만 좀 들이면 제곱근 표 만들 수 있습니다. 반복계산이라 지겹긴 하지만요.
요정도 계산은 엑셀이나 구글 스프레드시트가 잘 합니다. 소숫점으로 어디까지 나오는지 한 번 볼까요?
계산할 때에는 이미 별 도움 안 되는 거 확인한 정삼각형에서 시작하지 말고, 정육각형에서 시작하겠습니다. 한 변 길이가 1/2로 딱떨어지니 참 좋습니다.
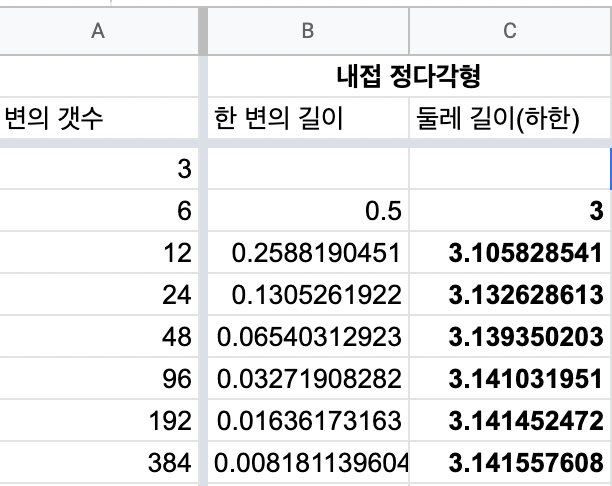
단 4번만에(놀랍죠?) 내접다각형의 길이 3.141이라는 하한값(lower bound)을 구할 수 있습니다.
방법이 조금 다릅니다. 식도 다르구요. 직각삼각형의 닮음을 이용해서 계산하게 되는데요. 한 번 해 보시죠. :)
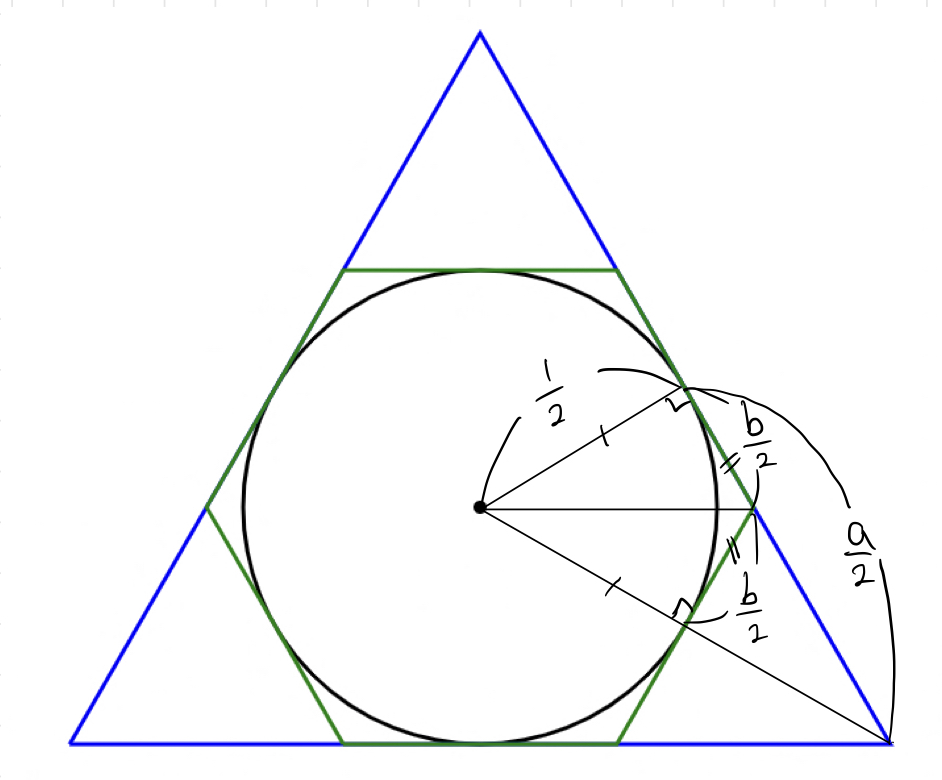
답은 알려드릴게요. 현재 정다각형의 한 변길이가 a이고 그 다음 정다각형의 한 변 길이를 b라고 할 때,
이것까지 이용해서 원주율의 하한값과 상한값을 모두 구글 스프레드시트로 구해보면,

오늘은 원 둘레길이를 구하는데 썼지만, 원래 이 방법은 적분법으로 더 많이 쓰였습니다. 옛날에 넓이 구하는 기술은 주로 정형화되어 있지 않은 땅의 넓이를 구하는데 쓰였는데, 일단 내접 삼각형을 땅 안에 넣은 다음에 빈 부분에 다시 삼각형을 집어 넣고, 다시 빈 부분에 삼각형을 집어넣는 것을 반복하면서 땅의 넓이를 근사적으로 구했더랬습니다.
이렇게 원주율값은 어디서 뚝 떨어진 것이 아니라 지금도 직관과 피타고라스 정리 몇 번 사용하는 것으로 아주 가까운 값까지 계산 가능한 것이랍니다. 끝.
