분수 곱셈시리즈의 거의 마지막입니다. 우리는 분수를 어떻게 곱하는 지 이미 압니다. 왜 그렇게 하는 지를 모를 뿐이죠. 결말을 알고 보는 영화는 재미가 없지만, 결론을 알고 보는 수학은 왠지 재미납니다. 한 번 볼까요.
분수와 분수를 곱하면 분자는 분자끼리, 분모는 분모끼리 곱한 다음에 필요하면 약분해서 답을 낸다는 것을 알고 있을 겁니다.
하지만 정작 저 곱셈의 정체는 무엇일까요?
우리가
분수와 분수의 곱셈을 이해하기 위해서는 다음과 같은 부분을 이해해야 합니다.
4 \div 3 = \frac43 즉, 자연수 나누기 자연수는 분수와 같다.
4÷3과 4/3왜 같을까? 에서 왜 그런지 짚어봤습니다. 이걸 1번 지식이라고 불러봅시다.
\frac23 \times 4= \frac{2 \times 4}{3} 분수를 자연수배(예를 들어 4배)하는 것은 분자랑 배수를 곱한 것과 같다.
2 / 3가 3개로 나눈 조각이 2개 있다는 뜻이니 그것의 4배는 그런 조각이 8개 있다는 뜻이겠지요. 분수를 보조눈금으로 이해하기 라는 글에서 설명했습니다. 이것을 2번 지식이라고 합시다.
그리고 이번 글에서 나머지 2가지를 더 알아보면 됩니다.
4 \times \frac23 즉, 4의 2/3배(자연수의 분수배)라는 게 무슨 뜻일까?, 이걸 알게 되면 3번 지식이라고 합시다.
\frac23 \div 2 즉, 분수를 자연수로 나누는 건 어떻게 할까? 이걸 알게 되면 4번 지식이라고 합시다.
피자 한 판의 2배는? 똑같은 피자를 두 판 모은 것.
두부 한 모의 2배는? 똑같은 두부를 두 모 모은 것.
이제 피자와 두부자리에 숫자를 넣어 봅시다.
2의 2배는? 2랑 똑같은 걸 두 개 모은 것. 2 x 2라고 씀. 계산하면 4
3의 2배는? 3이랑 똑같은 걸 두 개 모은 것. 3 x 2라고 씀. 계산하면 6
숫자로 넣어도 같은 방식이라는 걸 알 수 있습니다. 다만 말로 길게 쓴 것을 수식으로 간단하게 쓸 수 있고, 최종 값도 계산이 된다는 것만 다릅니다.
피자 한 판의 2/3는? 피자를 3조각으로 똑같이 나눈 다음, 그 중 2 조각을 취한 것
두부 한 모의 2/3는? 두부를 3조각으로 똑같이 나눈 다음, 그와 같은 조각을 2개 모은 것.
개념적으로는 저러했습니다. 저기의 피자와 두부 자리에 숫자를 넣어볼까요?
4의 2/3은? 4를 3조각으로 나눈다음 그것의 2배를 취한 것.4 \times \frac23 이라고 씀.
수식으로는 저렇게 씁니다. 계산도 가능하니, 지금까지 알고 있는 것으로 어떻게 계산이 되는지 따라가봅시다.
4를 3조각으로 나눈 다음 그것의 2배를 구하려고 보니,
4를 3조각으로 나눈 것은 4/3과 같다. (1번 지식 활용)
4/3은 1/3이라는 단위(눈금)으로 4칸을 잰 크기라는 것인데, 이것의 2배이니 같은 눈금이 4 x 2 칸만큼 모인 것이 될 것이다. (2번 지식 활용)
답은 1/3이라는 단위(눈금)이 8개 모인 것.
수식으로 나타내면 이렇게 됩니다.
자연수의 분수배(3번지식)은 이렇게 1번지식과 2번 지식의 조합으로 이해할 수 있습니다.
여기서 한 가지 더.
계산되는 방식을 보니 분모는 그대로 두고 자연수와 분자를 곱해서 답을 낸 것과 같다는 것을 알 수 있습니다. 그래서 2번지식(분수의 자연수배)와 지금 알게된 3번 지식 (자연수의 분수배)가 계산 방식이 결국 같아지고, 분수와 자연수는 순서를 바꾸어서 곱해도 답이 같구나(교환법칙 성립)라는 것도 알게 됩니다.
자연수의 분수배까지 이해했으니, 분수의 분수배도 똑같은 방법으로 할 수 있겠지요?
2/3의 4/5배라 함은, 2/3을 5로 똑같이 나눈 것을 4개 취한 것이다.
같은 방법으로 하면 되는데, 아직 파악하지 못한 부분이 여기서 나옵니다. 아직 2/3을 5로 나누는 걸 할 줄 모릅니다. 분수를 자연수로 나누는 것(4번 지식) 이것만 할 줄 알면 분수와 분수의 곱셈이 완성됩니다.
숫자를 좀 간단하게 해서, 2/3 을 자연수 2로 나누어봅시다.
2/3라는 것은 1/3이라는 보조눈금으로 재었을 때 2칸 먹은 크기입니다. 이것을 2로 나누는 것은 직관적으로 2칸 먹을 것을 반만 먹으라고 하면 되겠죠. 그래서
그런데 또 다른 방법이 있어요. 약간 야바위꾼 같은 이야기인데, 이렇게 하는 겁니다.
너 두 칸 먹어, 너 두 칸 똑같이 먹어 (전체 6칸 중에 말야)
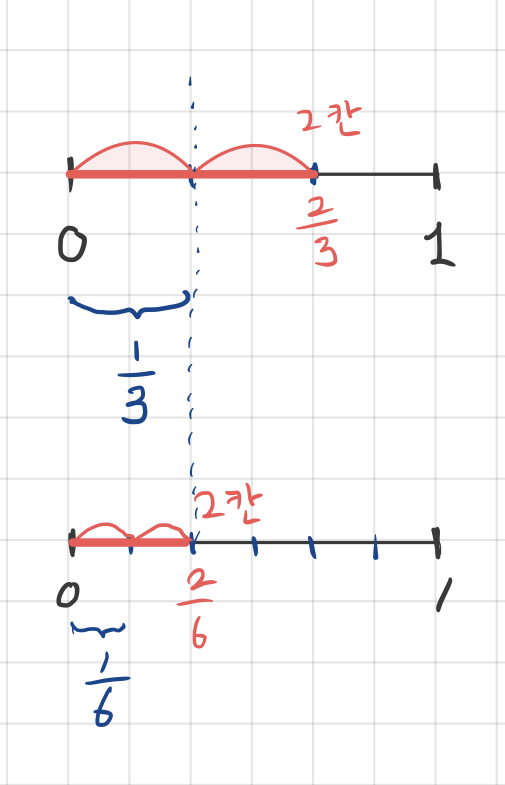
눈금 속이면 범죄라고 했는데, 똑같이 2칸 먹으라고 한 다음, 눈금 자체를 2배 더 오밀조밀한 것으로 바꿔버리는 것이죠. 그렇게 하면 같은 두 칸을 먹어도 눈금 갯수가 2배 늘어난 만큼 눈금 하나의 크기가 반으로 줄어버리기 때문에, 2를 나눈 것과 같은 효과가 납니다. 그래서
이 두가지 방법 중에서 우리가 주목하는 건 눈금을 바꿔버리는 두 번째 방법입니다. 즉 분수를 자연수로 나누면 분수의 분모에 자연수를 곱한 것과 같아진다는 것이지요. 이것이 4번 지식입니다.
다시 원래 문제로 돌아와서
2/3의 4/5배라 함은, 2/3을 5로 똑같이 나눈 것을 4개 취한 것이다.
2/3을 5로 똑같이 나누면\frac2{3 \times 5} 가 된다 (4번 지식)
\frac2{3 \times 5} 을 4배 하면\frac{2\times 4}{3 \times 5} 가 된다 (2번 지식)
그래서 답은 8/15
이것을 수식으로 쓰면,
몇 가지 다른 숫자에 대해서 해 보면 분수와 분수를 곱할 때, 결국 분자는 분자끼리, 분모는 분모끼리 곱한다는 걸 알게 됩니다.
분수와 분수 연산은 초등 산수에서 꽤 큰 고비입니다. 이것까지 이해하고 나면 숫자의 곱을 넓이로 나타내는 것에도 익숙해지고 도형과 숫자가 연결되는 맛을 느끼기도 쉬워지죠. 숫자를 숫자만으로 받아들이면 보통 재미가 없거든요. 도형의 넓이와 비율을 눈으로 보고 숫자랑 연결해서 보려면 분수라는 고비까지만 넘기면 됩니다. (물론 곧 무리수라는 장벽을 또 만납니다)
다음 글에는 중간에 잠시 멈췄던 분수 나누기 분수를 해 보겠습니다.
