왜 분수를 나누면 역수를 곱한 게 될까?

분수를 나누면 역수 취해서 곱하면 된다고들 배웠습니다. 계산이 간단하니 쉽게 적용할 수 있지만 도대체 왜 그렇게 해도 되는 걸까요?

드디어 분수의 나눗셈으로 돌아왔습니다. 잠시 지금까지 다루어왔던 것을 되짚어 보면, 나눗셈 a÷b 를 해석하는 방법이 두 가지 있었습니다.

<해석 1> a를 b명의 사람에게 나누어주면 한 사람의 몫은 얼마일까?

<해석 2> a를 b만큼씩 각 사람에게 나누어 주면 몇 사람에게 돌아갈까? 혹은, a안에는 b가 몇 번이나 들어갈까?

<해석 1>을 통해서 4 \div 3=\frac43 이 왜 같은 지 알 수 있었습니다. (4÷3과 4/3은 왜 같을까? 참조)

 4 \div \frac13 은 <해석 2>를 통해 보면 4 안에 \frac13 이 12번 들어가므로 답이 12라는 것을 알 수 있었지요. (분수로 나누면 왜 곱하기가 될까? 참조)

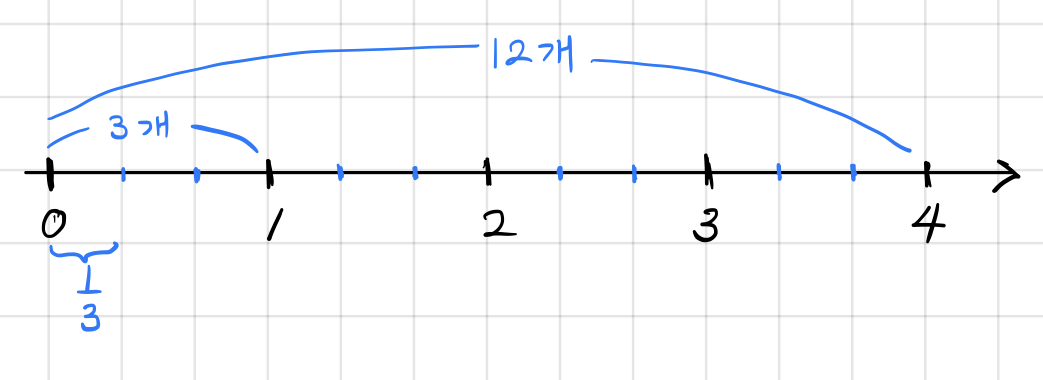
사실, <해석 2>를 계속 확장해 나가면 \frac52 \div \frac23 와 같은 나눗셈도

 \frac52 안에 \frac23 가 몇 번 들어가는가? 

로 해석을 한 다음, 답을

 \frac32 번의 \frac52 배가 되는 횟수만큼 들어간다

라고 할 수 있습니다. 하지만 거기까지 도달하기 전에 머리가 결리기 시작할 거에요. 우리가 사용하는 언어로는 \frac32 의 \frac52 배가 되는 횟수라는 것이 와닿지 않거든요.

새로운 해석

그래서 나눗셈의 새로운 해석을 하나 더 도입할 겁니다. 이 새로운 해석에 따르면 나눗셈 a÷b 라는 것은

<해석 3> b에다가 뭘 곱해야 a가 되는 지 찾는 것

이라고 볼 수 있습니다. 이 해석이 맞아들어가는지 이미 아는 나눗셈으로 확인해 볼까요?

12÷4란 4에 뭘 곱해야 12가 되는 지 찾는 것입니다. 3을 곱해야 12가 나오므로, 답은 3이 됩니다. 잘 맞아들어가죠? 기억을 더듬어보면 사실 우리가 처음 나눗셈을 배울 때 매번 하던 일이 이것이었습니다. 

12 안에 4가 몇 번 들어가지? 4×2는 8이고, 4×3은 12니까 딱 맞네, 3번 들어가네

 4 \div \frac13  은 \frac13 에 뭘 곱해야 4가 되는지를 찾는 것이죠. 분수의 곱셈과 기약분수(irreducible fraction)에 익숙하다면 답이 12라는 걸 알 수 있습니다. <해석 2>를 통해서 얻었던 답과 동일하죠. 이렇게 새로운 해석법<해석 3>은 분수 곱셈이 익숙해야 쉽게 적용할 수 있습니다. 

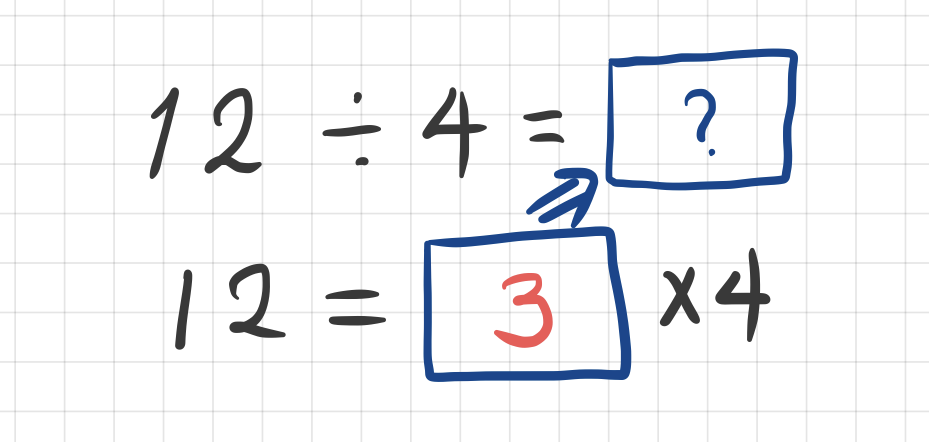
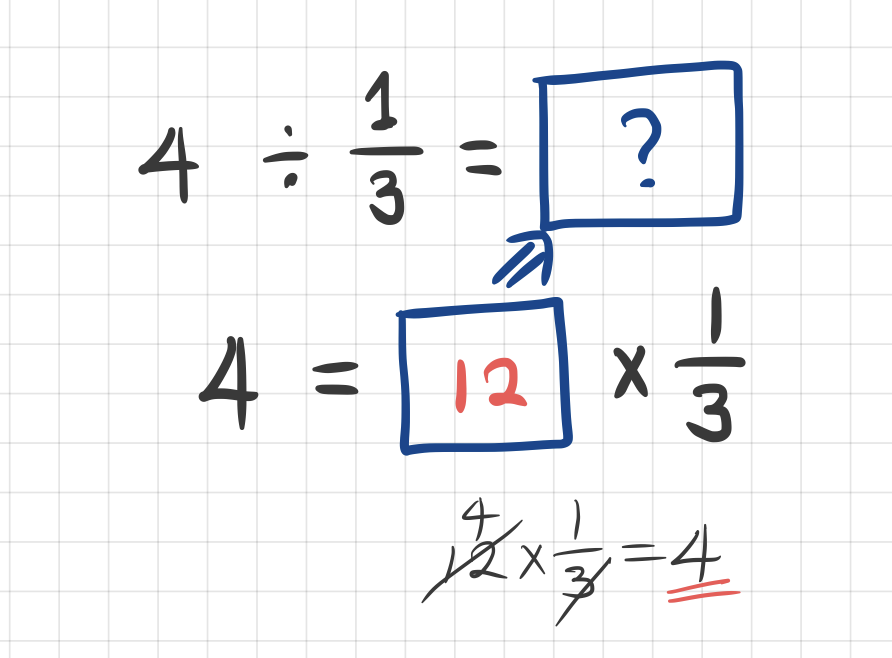
익숙해지기 위해서 가장 간단한 것부터 연습해 보겠습니다. 곱셈이든 나눗셈이든 1부터 시작하는 것이 연습하기에 좋습니다.

 1\div \frac23  는 <해석 3>에 의하면 \frac23 에 뭘 곱해야 1이 되는지를 찾는 것과 같습니다. 곱해서 1이 되는 것을 찾는 것은 쉽지요. 역수(분자와 분모의 자리를 바꾼 분수, reciprocal)를 곱하면, 약분이 익숙한 사람의 눈에는 싹 약분되고 1밖에 안 남아서 1이 되고, 약분이 익숙하지 않은 사람에게도 그냥 곱하면 분자 분모의 숫자가 똑같아지니 결국 1이 된다는 것을 쉽게 알 수 있습니다. 그래서 어떤 분수를 두고 무언가를 곱해서 1을 만들고 싶으면 역수를 곱하면 됩니다.

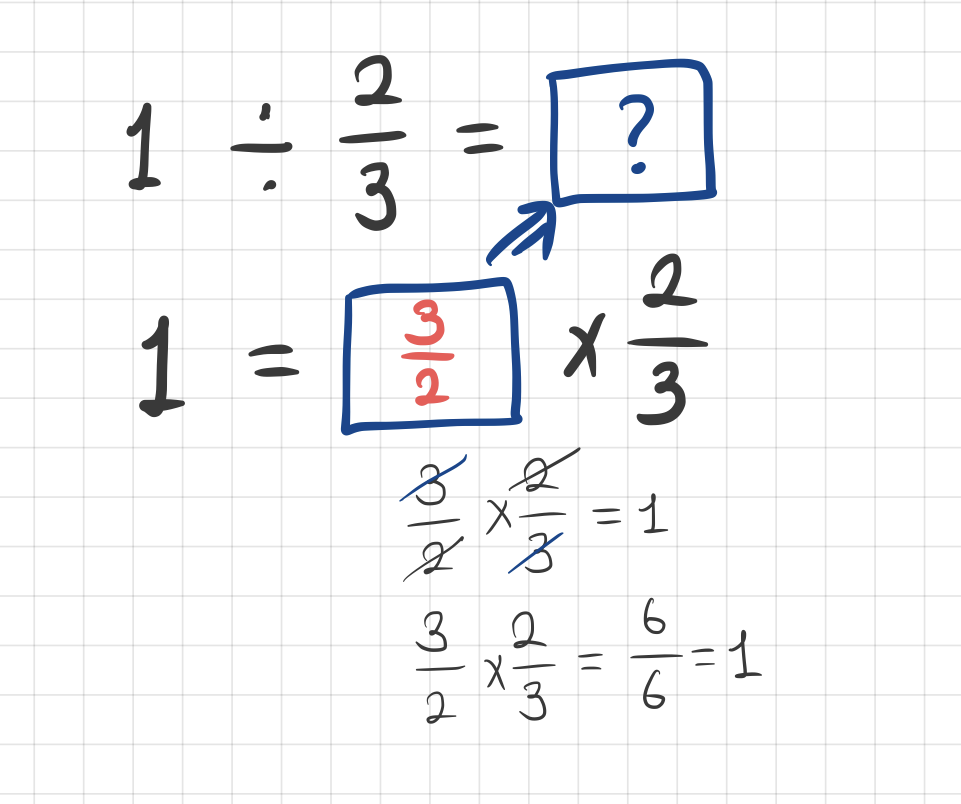
이제 1이 아닌 다른 수로 확장해 보겠습니다.

 \frac52 \div \frac23  

 \frac23 에 뭘 곱해야 \frac52 가 될까요? 방법은 간단합니다. 일단 \frac23 에 무언가 곱해서 1로 먼저 바꾸고, 그 값에 다시 무언가를 곱해서 \frac52 로 바꿉니다. 곱해서 1로 만들고 싶다면, 역수인 \frac32 를 곱하면 되겠죠. 그렇게 해서 만들어진 1을 \frac52 로 바꾸는 과정은 아주 쉽습니다. 다시 거기에 \frac52 를 곱하면 되죠. 그래서 답은 역수 \frac32 와 원래 숫자 \frac52 를 곱한 수가 되는 것입니다.

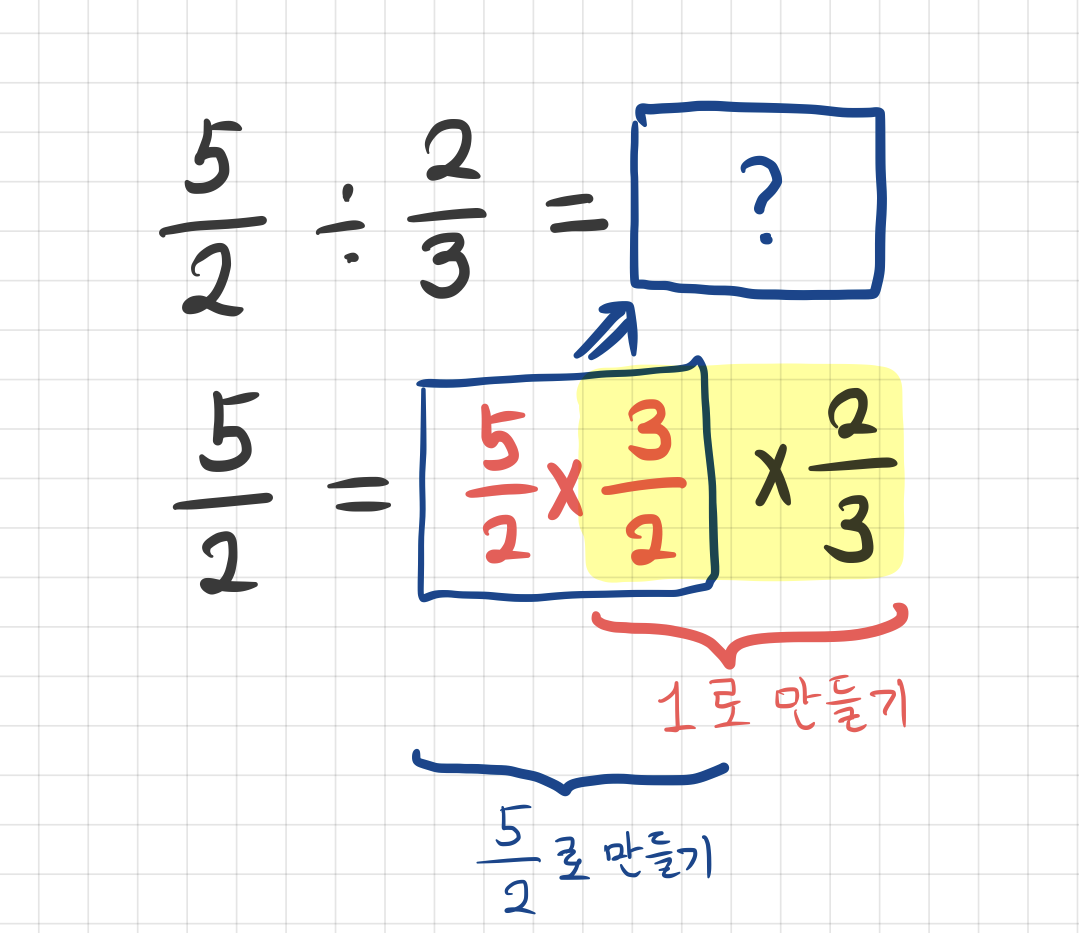
여기서 역수와 원래숫자를 곱한 것이 나왔다는 것에 주목해 봅시다. 몇 가지 다른 숫자에 대해서 해 보아도 답이 항상 역수와 원래 숫자를 곱한 것과 같다는 것을 알게 됩니다.

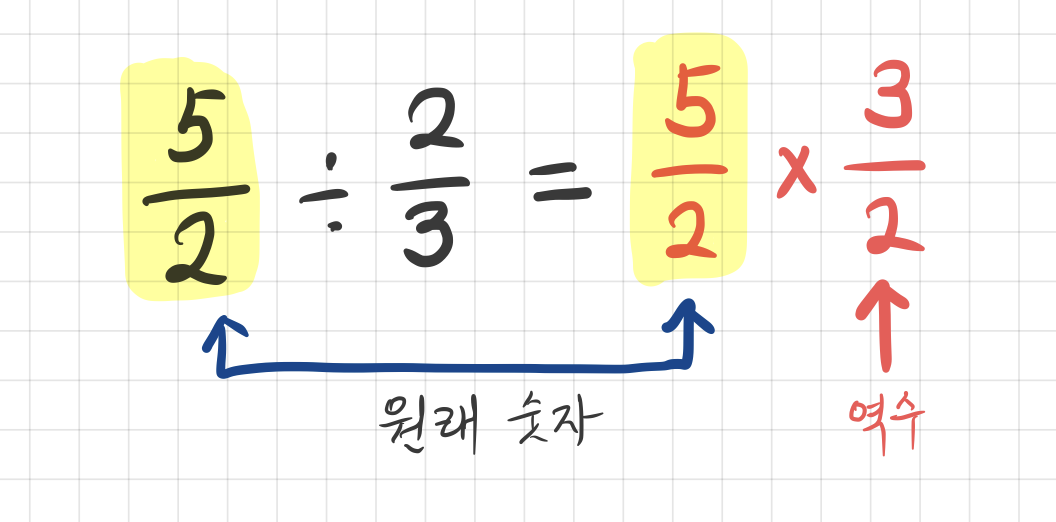
어떤 나눗셈이든 역수를 곱한 것으로 생각할 수 있기 때문에, 이 사실을 안 이후부터는 나눗셈 기호를 (거의) 쓰지 않고 역수의 곱셈으로 대체합니다.

에필로그

이렇게 나눗셈 기호 ÷는 우리 어린시절 추억으로만 남게 되는 것이죠. 숫자의 범위가 넓어지면서 나눗셈이 어떤 다른 숫자의 곱셈과 같다는 것을 알게 되는 것은 아주 큰 도약입니다. 교과서 만드시는 분들은 이 즈음에 항등원(identity)와 역원(inverse)의 개념을 어떻게든 설명해 버릴까? 아니면 그냥 하지 말까? 많은 고민을 했을런지도 몰라요. 이 단계에서는 이름은 크게 중요하지 않으니 외울 필요는 없고, 한 번 흘러가듯이 들어만 보겠습니다.

항등원과 역원 

아까 중요한 숫자가 두 개 있었습니다. 곱셈이든 나눗셈이든 1에서 시작해서 확장하는 것이 쉽다고 했었죠. 그리고 분수로 나누는 것은 역수를 곱하는 것과 같다고 했었지요. 이렇게 특별한 성질이 있는 숫자에는 이름이 붙습니다. 1은 곱셈의 항등원(identity)입니다.

곱셈의 항등원이란 무슨 숫자에 곱하든 항상 그 원래 숫자가 나오게 만드는 넘

을 말합니다. 직관적으로 1이죠. 뭔가에 1을 곱하면 값이 안 바뀌고 원래 숫자가 그대로 답이 되지요.

글씨가 지렁이 기어가는 것 같은 이유는 아이패드 유리가 미끄러워서 그런 거에요

 역수(reciprocal)는 곱셈의 역원(multiplicative inverse)입니다. 

곱셈의 역원이란 어떤 숫자에 곱했을 때 항등원(곱셈에서는 1)을 만들어주는 넘

아까 앞에서 어떤 숫자에 뭔가 곱해서 1이 되게 만드려면 역수(분모 분자 바꾼 수)를 곱하면 된다고 했지요. 그래서 곱셈의 역원은 역수가 됩니다. 

이걸 왜 안 가르칠까요? 새로운 이름 외우는 건 귀찮아서 그런 것이기도 하고요. 나름대로의 고충이 있습니다. 예를 들어, 우리가 짝수가 무엇인가에 대해서 배웠을 때에는, 짝수가 무한히 많고(2, 4, 6, 8, ...) 그와 대비해서 보여줄 홀수도 무한히 많아서(1, 3, 5, 7, ...) 배우는 사람이 감을 잡기가 훨씬 쉬웠습니다. 하지만 항등원과 역원은 그렇지 않아요. 기껏 아는 연산이 4개 밖에 없는데(더하기, 빼기, 곱하기, 나누기) 나눗셈은 앞에서 보았던 것 처럼 곱셈으로 해석이 되고, 뺄셈은 음수의 덧셈로 해석할 수 있게 되어서 실질적인 연산이 덧셈과 곱셈 2개 밖에 없습니다. 그래서 항등원과 역원도 각각 2개씩 밖에 안 나오죠. 예제가 2개밖에 없는 것에 대해서 무언가를 정의하면 많은 아이들이 그것의 의미를 알려고 하기보다는 그냥 예제를 외우게 됩니다.

"항등원은 1이다" 이런 식으로 외워버리죠. 이것은 엄청난 부작용입니다. 사실 곱셈의 항등원이 1인 것이고, 덧셈의 항등원은 0이고, 연산 따라 항등원은 달라지는데 말이에요. 그래서 이런 용어와 개념은 연산을 좀 더 배워서 예시가 좀 더 다양해지면 그 때 다시 짚어보겠습니다. 일단 스쳐가듯, 이름만 한 번 눈에 익혀봅시다. 끝.